こんにちは。中学受験情報局 算数主任の前田昌宏です。

今日は速さの10回目として、「速さの応用問題は確かに難しいのですが…」というテーマです。

速さの応用問題は本当に難物だと思います。

でも入試のことを考えると逃げてばかりもいられません。

そこで『本物の難題』はさておき、
難しそうだけど何とかなりそうな問題に、どんな問題があるかを探ってみましょう。

「難しそうに見えますが、この手の問題は○○すれば何とかなる！」の一番手は…
通過算！

通過算のポイントは6月6日のブログでも書いたように、
「絵をかけば解けるはずだ！」です。

今日はその絵のどこに着目するとよいかについて書いてみます。

【問題】
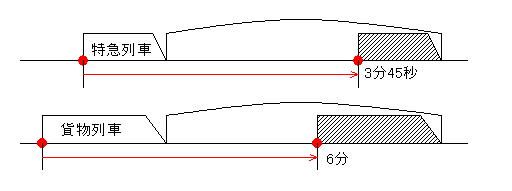
あるトンネルで、列車の先端が入ってから先端が出るまでの時間を計ったところ、特急列車は3分45秒、貨物列車は6分でした。特急列車の速さは、貨物列車の速さより毎時45km速いです。このとき、トンネルの長さは□ｍです。（灘中）

でました、灘中！

といっても、灘中の問題全てが超難問というわけではないんです。
この問題のように、5年生でも取り組める問題もあるんですね。

まず、
「先端が入ってから先端が出るまでの時間を計ったところ、特急列車は3分45秒」と
「先端が入ってから先端が出るまでの時間を計ったところ、貨物列車は6分」を
絵にします。

図①

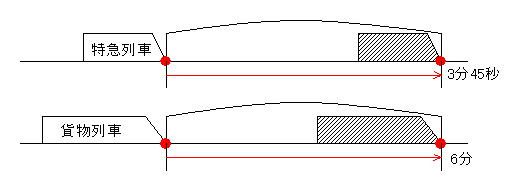
図②

ところでお子さんの図はどちらですか？

いつも「列車の後ろ」を見ているから、今回も！

というお子さんは図②でしょうか？

通過算の絵には大切なコツがあります。

「列車が移動後に接している部分に着目する」ということです。

この問題の場合、
列車が移動して、その「先端」がトンネルの出口と接触していますから、
「列車の先端」部分がどう動いたかを線分図にすると…、

図②のようになります。

さて、「線分図は距離の条件を利用する」が大原則でしたね？

この原則に従って図②をみると、
「どちらも移動距離が同じ」
ということに気づけます。

（図②の方が気づきやすいでしょ？）

距離が同じ場合は、時間の比と速さの比とは逆比の関係ですから、

時間の比　特急：貨物＝5：8
↓
速さの比　特急：貨物＝⑧：⑤
速さの差③＝時速45km　より、貨物列車の速さは時速75kmとわかります。

ここでもう一度絵を見ると、求めたいトンネルの長さと「→」が同じですから、
時速75km　×　6/60時間　＝　7.5km　→　答え　7500（m）

通過算の場合は、「速さと比」の関係が比較的わかりやすいので、
まずは通過算で自信をつけると上手くいきそうですね。