『速さ 中級レベルの学習ポイント』2
第153回 入試の定番問題を攻略しよう ~6~

「女子学院中学校 26年度用―中学過去問シリーズ (10年間スーパー過去問7) 」声の教育社
定番の問題で失点しないことが合格の条件というテーマでお話をしています。
前回は中級レベルに入る前提として「定番の問題」の基本レベルをみました。
今回の題材はいよいよ本題の「速さ(中級レベル)」です。
基本レベルの力がどう関わってくるのかをみていきたいと思います。
今回の定番問題は中級レベルで失点するお子さんにとって
チェック問題としても活用できます。
入試問題を例題としていますが、5年生でもチャレンジ可能な問題です。
2013年度 女子学院中学 入試問題 大問4
4.流れの速さが時速3.3kmの川の上流にA地点、下流にB地点があり、4015m離れています。J校のボートの長さは2.6m、G校のボートの長さは2.4mです。
(1)ある日、J校のボートがA地点から下流に向かって、G校のボートがB地点から上流に向かって同時に出発し、6分後にすれ違い終わりました。この日のJ校のボートの静水(流れのないところ)での速さは時速21kmです。G校のボートの静水での速さは時速何kmでしたか。
(2)次の日、J校とG校のボートが、A地点から下流に向かって同時に出発しました。この日のJ校のボートの静水での速さは時速19.8kmです。G校のボートは、はじめJ校のボートより毎分5m遅かったのですが、途中からの静水での速さで4%速くしたので、B地点から11m上流のところで2校のボートの先端が並びました。G校のボートが速さを変えたのはA地点から何mのところですか。
流水算です。
流水算の基本は
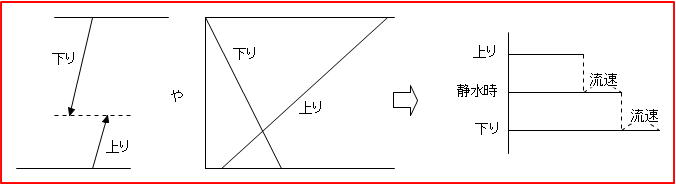
のように、線分図やダイヤグラムと速さの関係を整理することです。
こういった基本レベルのことがらを旅人算、時計算、通過算など「速さ」の問題だけでなく、
数の問題や図形の問題、場合の数などでも問題を解くとき、常に意識するようにします。
「この形に持ち込めれば答えが必ず出る!」という意識です。
さて(1)は時間の条件だけがあるので原則はダイヤグラムに整理するのですが、
「ボートの長さ」をダイヤグラムに表すことは難しいので、
「電車の長さ」が関わっている通過算のように、線分図に整理する方が良い問題です。
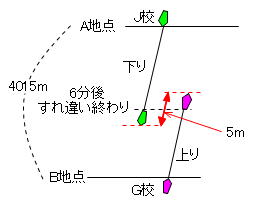
この図から次の3つのことが順番にわかればOKです。
1.旅人算(すれ違い→出会いパターン)の考え方が使える
2.赤い矢印に着目すると、2隻の進んだ距離の和は4015m+5m=4020m
3.出会いの流水算では、2隻の静水時の速さの和=上りの速さ+下りの速さ
ひとつひとつは定番問題の基本レベルの公式です。
しかし中級レベルになると、それらが複数組み合わさっているんですね。
この組み合わせの正体をひとつずつ順番に図から読み取ると、
4020m÷6分=分速670m=時速40.2km…上りの速さ+下りの速さ=静水時の速さの和
時速40.2km-時速21km=時速19.2km
と求められます。
基本レベルを解いているときにただ公式を覚えるだけでなく、
線分図やダイヤグラム、あるいは表などと一緒にして学習する=理解することで、
このような中級レベルの定番問題を短時間に攻略することが可能になっていきます。
(2)は距離の条件だけなので線分図に整理してみましょう。
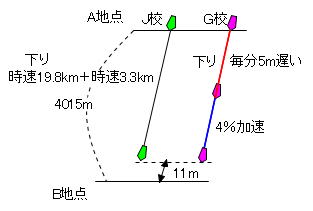
受験生ならば、この「途中で変速する線分図」は「速さのつるかめ算」でおなじみすよね。
もし、この図が書けるのに「つるかめ算だ!」と気づけないお子さんは、
基本レベルの学習が「理解」につながっていない可能性があります。
「問題文を自分で線分図にし、
その線分図をみながらつるかめ算で解く」という学習方法が、
「理解」には必要なのですが、
これが5年生段階で欠けていたのかもしれません。
受験生は今ならば「できるようになりたい」という意識が高まっていますから、
もう一度正しい学習方法に取り組むことができますので、
苦手分野では基本レベルから、少しはできる分野であるならば、
このくらいの中級レベルで試してみて下さい。
さて、解き方に戻ります。
時速23.1km×1000÷60=分速385m…J校
4004m÷分速385m=10.4分…2隻の先端が並ぶまでの時間
分速385m-分速5m=分速380m…はじめのG校
時速3.3km×1000÷60=分速55m…川の流れ
分速380m-分速55m=分速325m…G校の静水時
分速325m×1.04=分速338m
分速338m+分速55m=分速393m…あとのG校
ここまで求めたら、あとはつるかめ算なので
(分速393m×10.4分-4004m)÷(分速393m-分速380m)=6.4分
…G校が速さを変えるまでの時間
分速380m×6.4分=2432m
と求められます。
ここでも中級レベルの定番問題である、
「流水算の基本+つるかめ算の基本」といった基本レベルの組み合わせとなっていますね。
「中級レベルは基本レベルの組み合わせだ」
「基本レベルが理解(暗記はダメ!)できれば大丈夫」
という中級レベル攻略法を意識できれば、
少しくらいの長文問題でも平気で対応ができるようになります。
中級レベルの正体を知ることが、中級レベルの攻略法でもあるのです。
ところでこの問題、速さのつるかめ算をダイヤグラムに整理してみると…
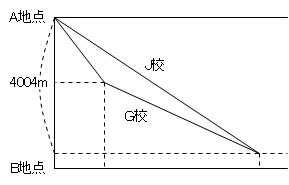
そうですね! これって、前回の平均の速さと同じかたちのグラフです。
平均の速さは「てんびん法」が使えましたから、
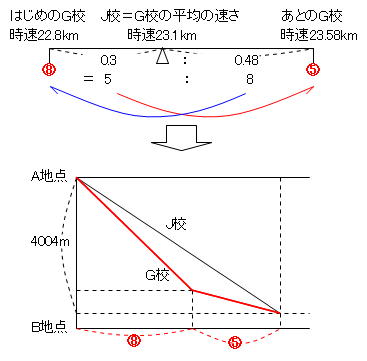
となります。
ということは、はじめのG校の速さ×速さを変えるまでの時間=(2)に解答 ですから、
時速22.8km×{(4.004km÷時速23.1km)×8/13}×1000
=22.8/1×4.004/23.1×8/13×1000 ←4.004と23.1が11で割り切れます
=228/1×0.364/2.1×8/13×100
=228/1×364/2100×8/13×100 ←228と2100が3の倍数です
=76/1×364/700×8/13×100
=76/1×364/7×8/13 ←364は7の倍数です
=76/1×52/1×8/13 ←52は13の倍数です
=76×4×8
=2432m
のように、約分をしながら計算をすすめることができます。
このように書かれると面倒なように見えますが、
実際には次のようなかんじで問題用紙などに書きますから、
計算が楽になります。
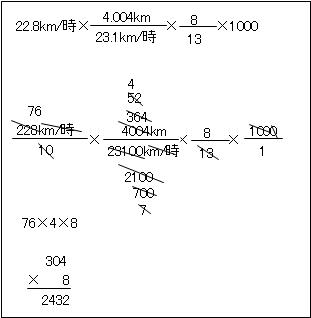
「分母の7がなくなってくれるといいのになぁ。」や
「お、11の倍数があるぞ! もしかしたら約分できるかも…」
のように期待を込めながらふだんの計算問題で練習を積んで、
消えそうな数字の組み合わせを知識としてもっておくと、
このような問題でも役に立ちます。
定番の基本レベルで出てきた「計算の工夫」が中級レベルでも役に立つわけです。
ですから定番の中級レベルの攻略法で大切なことは、
中級レベルが基本レベルの組み合わせであることを頭において、
基本問題を解くときに
・「公式や計算の意味を理解して覚える(図や表と結びつけて整理ができる)」こと、
・「計算の工夫ができる」こと、
の2点を実行し続けることなのです。


「女子学院中学校 26年度用―中学過去問シリーズ (10年間スーパー過去問7) 」声の教育社
定番の問題で失点しないことが合格の条件というテーマでお話をしています。
前回は中級レベルに入る前提として「定番の問題」の基本レベルをみました。
今回の題材はいよいよ本題の「速さ(中級レベル)」です。
基本レベルの力がどう関わってくるのかをみていきたいと思います。
今回の定番問題は中級レベルで失点するお子さんにとって
チェック問題としても活用できます。
入試問題を例題としていますが、5年生でもチャレンジ可能な問題です。
2013年度 女子学院中学 入試問題 大問4
4.流れの速さが時速3.3kmの川の上流にA地点、下流にB地点があり、4015m離れています。J校のボートの長さは2.6m、G校のボートの長さは2.4mです。
(1)ある日、J校のボートがA地点から下流に向かって、G校のボートがB地点から上流に向かって同時に出発し、6分後にすれ違い終わりました。この日のJ校のボートの静水(流れのないところ)での速さは時速21kmです。G校のボートの静水での速さは時速何kmでしたか。
(2)次の日、J校とG校のボートが、A地点から下流に向かって同時に出発しました。この日のJ校のボートの静水での速さは時速19.8kmです。G校のボートは、はじめJ校のボートより毎分5m遅かったのですが、途中からの静水での速さで4%速くしたので、B地点から11m上流のところで2校のボートの先端が並びました。G校のボートが速さを変えたのはA地点から何mのところですか。
流水算です。
流水算の基本は

のように、線分図やダイヤグラムと速さの関係を整理することです。
こういった基本レベルのことがらを旅人算、時計算、通過算など「速さ」の問題だけでなく、
数の問題や図形の問題、場合の数などでも問題を解くとき、常に意識するようにします。
「この形に持ち込めれば答えが必ず出る!」という意識です。
さて(1)は時間の条件だけがあるので原則はダイヤグラムに整理するのですが、
「ボートの長さ」をダイヤグラムに表すことは難しいので、
「電車の長さ」が関わっている通過算のように、線分図に整理する方が良い問題です。

この図から次の3つのことが順番にわかればOKです。
1.旅人算(すれ違い→出会いパターン)の考え方が使える
2.赤い矢印に着目すると、2隻の進んだ距離の和は4015m+5m=4020m
3.出会いの流水算では、2隻の静水時の速さの和=上りの速さ+下りの速さ
ひとつひとつは定番問題の基本レベルの公式です。
しかし中級レベルになると、それらが複数組み合わさっているんですね。
この組み合わせの正体をひとつずつ順番に図から読み取ると、
4020m÷6分=分速670m=時速40.2km…上りの速さ+下りの速さ=静水時の速さの和
時速40.2km-時速21km=時速19.2km
と求められます。
基本レベルを解いているときにただ公式を覚えるだけでなく、
線分図やダイヤグラム、あるいは表などと一緒にして学習する=理解することで、
このような中級レベルの定番問題を短時間に攻略することが可能になっていきます。
(2)は距離の条件だけなので線分図に整理してみましょう。

受験生ならば、この「途中で変速する線分図」は「速さのつるかめ算」でおなじみすよね。
もし、この図が書けるのに「つるかめ算だ!」と気づけないお子さんは、
基本レベルの学習が「理解」につながっていない可能性があります。
「問題文を自分で線分図にし、
その線分図をみながらつるかめ算で解く」という学習方法が、
「理解」には必要なのですが、
これが5年生段階で欠けていたのかもしれません。
受験生は今ならば「できるようになりたい」という意識が高まっていますから、
もう一度正しい学習方法に取り組むことができますので、
苦手分野では基本レベルから、少しはできる分野であるならば、
このくらいの中級レベルで試してみて下さい。
さて、解き方に戻ります。
時速23.1km×1000÷60=分速385m…J校
4004m÷分速385m=10.4分…2隻の先端が並ぶまでの時間
分速385m-分速5m=分速380m…はじめのG校
時速3.3km×1000÷60=分速55m…川の流れ
分速380m-分速55m=分速325m…G校の静水時
分速325m×1.04=分速338m
分速338m+分速55m=分速393m…あとのG校
ここまで求めたら、あとはつるかめ算なので
(分速393m×10.4分-4004m)÷(分速393m-分速380m)=6.4分
…G校が速さを変えるまでの時間
分速380m×6.4分=2432m
と求められます。
ここでも中級レベルの定番問題である、
「流水算の基本+つるかめ算の基本」といった基本レベルの組み合わせとなっていますね。
「中級レベルは基本レベルの組み合わせだ」
「基本レベルが理解(暗記はダメ!)できれば大丈夫」
という中級レベル攻略法を意識できれば、
少しくらいの長文問題でも平気で対応ができるようになります。
中級レベルの正体を知ることが、中級レベルの攻略法でもあるのです。
ところでこの問題、速さのつるかめ算をダイヤグラムに整理してみると…

そうですね! これって、前回の平均の速さと同じかたちのグラフです。
平均の速さは「てんびん法」が使えましたから、

となります。
ということは、はじめのG校の速さ×速さを変えるまでの時間=(2)に解答 ですから、
時速22.8km×{(4.004km÷時速23.1km)×8/13}×1000
=22.8/1×4.004/23.1×8/13×1000 ←4.004と23.1が11で割り切れます
=228/1×0.364/2.1×8/13×100
=228/1×364/2100×8/13×100 ←228と2100が3の倍数です
=76/1×364/700×8/13×100
=76/1×364/7×8/13 ←364は7の倍数です
=76/1×52/1×8/13 ←52は13の倍数です
=76×4×8
=2432m
のように、約分をしながら計算をすすめることができます。
このように書かれると面倒なように見えますが、
実際には次のようなかんじで問題用紙などに書きますから、
計算が楽になります。

「分母の7がなくなってくれるといいのになぁ。」や
「お、11の倍数があるぞ! もしかしたら約分できるかも…」
のように期待を込めながらふだんの計算問題で練習を積んで、
消えそうな数字の組み合わせを知識としてもっておくと、
このような問題でも役に立ちます。
定番の基本レベルで出てきた「計算の工夫」が中級レベルでも役に立つわけです。
ですから定番の中級レベルの攻略法で大切なことは、
中級レベルが基本レベルの組み合わせであることを頭において、
基本問題を解くときに
・「公式や計算の意味を理解して覚える(図や表と結びつけて整理ができる)」こと、
・「計算の工夫ができる」こと、
の2点を実行し続けることなのです。




