『2014年度 中学入試速報』4
第167回 2014年度入試 ~4~

灘中 2014年度入試 算数 1日目(その2)
2014年度入試速報の第4回は灘中(その2)です。
「今年は1日目が比較的取り組みやすい問題でした」と前回書いたのですが、
しかしそこは灘中です。しっかり「難問」も出題されていました。
その中でも特に難しかったと思われる問題は、大問5-②と大問11 の2問です。
そこで今回は大問11をご紹介します。
確かに難問だったのですが、
灘中の過去問演習を解いていれば
「もしかしたら、あの方法が使えるかも…?」
と気づけたお子さんもいたのではないかと思います。
2014年 灘中 第1日 大問11(1日目の最終問題です。)
 11 右の図のように、長方形の板から大小2つの直角二等辺三角形の部分を切り取った板片があります。ただし、板の厚さは考えないものとします。この板片を直線アのまわりに1回転させたとき、板片が通過する部分の体積は□cm3です。
11 右の図のように、長方形の板から大小2つの直角二等辺三角形の部分を切り取った板片があります。ただし、板の厚さは考えないものとします。この板片を直線アのまわりに1回転させたとき、板片が通過する部分の体積は□cm3です。
もし、直角二等辺三角形を切りとらなければ円柱ができますので、
方針は「円柱の体積-切り取られた立体の体積」です。
しかし、
切り取られる直角二等辺三角形が「回転の軸から離れている」ため、
計算がとても大変そうですね。
こんなときに役立つのが、「回転体の体積比」でした。
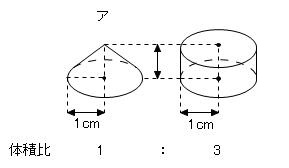
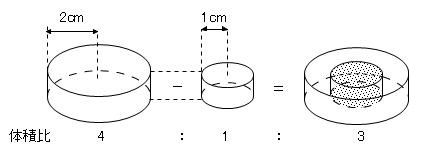
これらと相似な図形の体積比を利用すると、
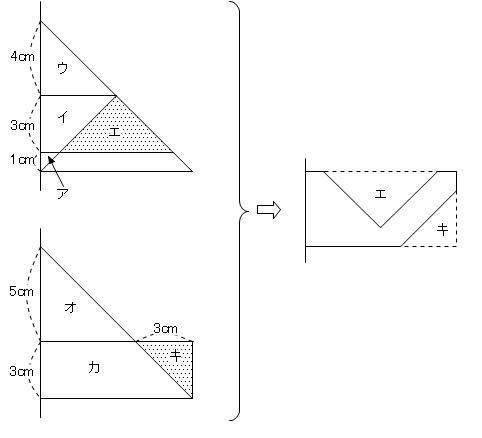
となるのでこの図から、
アの体積=1 とすると、
ウの体積=4×4×4=64
イの体積=ウ-ア=63
エの体積=7×7×7-(64+63)=216
オの体積=5×5×5=125
カの体積=8×8×8-125=387
キの体積=アの体積1×3×3×64-387=189
求める部分の体積=アの体積1×3×4×64-(216+189)=363
となり、アの体積の363倍ですから、
1cm×1cm×3.14×1cm×1/3×363=379.94cm3が答えとわかります。
少し大変な計算でしたが、

の応用問題だということは気づけたと思いますので、
「方針立て」で迷うことはなかったと思います。
ところで、上のような問題演習をしたときに、
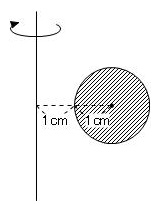
のような入試問題についても練習したかもしれません。
その解き方は「センターライン解法」の応用でした。
「センターライン解法」は、
円の面積の公式についての説明や、
次の図のような「円が通ったあとにできる図形の面積」の問題演習時に
学んだことがあると思います。
【問題】
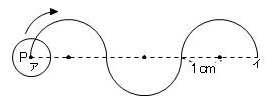
直径1cmの円があり、その円の中心Pが図の曲線(合田な半円3つを組み合わせた図形)上を通ったあとにできる図形の面積を求めなさい。
【センターライン解法による解き方】
2cm×π×1/2×3=3×π…曲線の長さ(センターラインの長さ)
1/2cm×1/2cm×π=1/4×π…始点と終点の半円の面積の和
1cm×(3×π)=3×π…移動する円の直径×センターライン=通った面積
(1/4+3)×π=3.25×3.14=10.205cm2
これを習ったときの説明と同じような説明で上記の「円の回転移動」も、
「円が回転してできる立体の体積
(1cm×1cm×π)×(4cm×π)=39.4384cm3
この方法が使えることに気づいたお子さんは、
この大問11でも時間をあまり使わずにすみます。
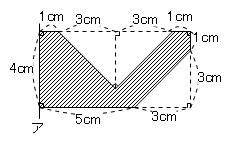
長方形の面積×長方形の重心の移動距離
-(直角二等辺三角形(大)の面積×直角二等辺三角形(大)の重心の移動距離
+直角二等辺三角形(小)の面積×直角二等辺三角形(小)の重心の移動距離)
という式で計算します。
長方形…(4cm×8cm)×(8cm×π)=256×π
直角二等辺三角形(大)…(6cm×3cm×1/2)×(8cm×π)=72×π
直角二等辺三角形(小)…(3cm×3cm×1/2)×(14cm×π)=63×π
(256-72-63)×3.14=121×3.14=379.94cm3
この「センターライン解法」を立体図形で利用する問題は
灘中以外にもいくつかの学校でこれまでに出題されていますが、
平面図形ほど多くはありません。
今回初めてこの解法にふれた新6年生のお子さんは、
通常の解き方をマスタース終えた後で、
「円が通ったあとにできる図形の面積」を
センターライン解法でチャレンジしてみましょう。
(※「どんな問題でもこの解法が使える」というわけでないところも、
大切な学習ポイントです。)
1つのテーマに対していくつもの解き方を持っていると、
今日ご紹介したような大変な問題でも、
より短時間に正確な答えをだすことができます。


灘中 2014年度入試 算数 1日目(その2)
2014年度入試速報の第4回は灘中(その2)です。
「今年は1日目が比較的取り組みやすい問題でした」と前回書いたのですが、
しかしそこは灘中です。しっかり「難問」も出題されていました。
その中でも特に難しかったと思われる問題は、大問5-②と大問11 の2問です。
そこで今回は大問11をご紹介します。
確かに難問だったのですが、
灘中の過去問演習を解いていれば
「もしかしたら、あの方法が使えるかも…?」
と気づけたお子さんもいたのではないかと思います。
2014年 灘中 第1日 大問11(1日目の最終問題です。)
 11 右の図のように、長方形の板から大小2つの直角二等辺三角形の部分を切り取った板片があります。ただし、板の厚さは考えないものとします。この板片を直線アのまわりに1回転させたとき、板片が通過する部分の体積は□cm3です。
11 右の図のように、長方形の板から大小2つの直角二等辺三角形の部分を切り取った板片があります。ただし、板の厚さは考えないものとします。この板片を直線アのまわりに1回転させたとき、板片が通過する部分の体積は□cm3です。もし、直角二等辺三角形を切りとらなければ円柱ができますので、
方針は「円柱の体積-切り取られた立体の体積」です。
しかし、
切り取られる直角二等辺三角形が「回転の軸から離れている」ため、
計算がとても大変そうですね。
こんなときに役立つのが、「回転体の体積比」でした。


これらと相似な図形の体積比を利用すると、

となるのでこの図から、
アの体積=1 とすると、
ウの体積=4×4×4=64
イの体積=ウ-ア=63
エの体積=7×7×7-(64+63)=216
オの体積=5×5×5=125
カの体積=8×8×8-125=387
キの体積=アの体積1×3×3×64-387=189
求める部分の体積=アの体積1×3×4×64-(216+189)=363
となり、アの体積の363倍ですから、
1cm×1cm×3.14×1cm×1/3×363=379.94cm3が答えとわかります。
少し大変な計算でしたが、

の応用問題だということは気づけたと思いますので、
「方針立て」で迷うことはなかったと思います。
ところで、上のような問題演習をしたときに、

のような入試問題についても練習したかもしれません。
その解き方は「センターライン解法」の応用でした。
「センターライン解法」は、
円の面積の公式についての説明や、
次の図のような「円が通ったあとにできる図形の面積」の問題演習時に
学んだことがあると思います。

【問題】
直径1cmの円があり、その円の中心Pが図の曲線(合田な半円3つを組み合わせた図形)上を通ったあとにできる図形の面積を求めなさい。
【センターライン解法による解き方】
2cm×π×1/2×3=3×π…曲線の長さ(センターラインの長さ)
1/2cm×1/2cm×π=1/4×π…始点と終点の半円の面積の和
1cm×(3×π)=3×π…移動する円の直径×センターライン=通った面積
(1/4+3)×π=3.25×3.14=10.205cm2
これを習ったときの説明と同じような説明で上記の「円の回転移動」も、
「円が回転してできる立体の体積
=円の面積×円の中心が軸のまわりに回転した距離」
という計算方法があることを習ったことでしょう。(1cm×1cm×π)×(4cm×π)=39.4384cm3
この方法が使えることに気づいたお子さんは、
この大問11でも時間をあまり使わずにすみます。

長方形の面積×長方形の重心の移動距離
-(直角二等辺三角形(大)の面積×直角二等辺三角形(大)の重心の移動距離
+直角二等辺三角形(小)の面積×直角二等辺三角形(小)の重心の移動距離)
という式で計算します。
長方形…(4cm×8cm)×(8cm×π)=256×π
直角二等辺三角形(大)…(6cm×3cm×1/2)×(8cm×π)=72×π
直角二等辺三角形(小)…(3cm×3cm×1/2)×(14cm×π)=63×π
(256-72-63)×3.14=121×3.14=379.94cm3
この「センターライン解法」を立体図形で利用する問題は
灘中以外にもいくつかの学校でこれまでに出題されていますが、
平面図形ほど多くはありません。
今回初めてこの解法にふれた新6年生のお子さんは、
通常の解き方をマスタース終えた後で、
「円が通ったあとにできる図形の面積」を
センターライン解法でチャレンジしてみましょう。
(※「どんな問題でもこの解法が使える」というわけでないところも、
大切な学習ポイントです。)
1つのテーマに対していくつもの解き方を持っていると、
今日ご紹介したような大変な問題でも、
より短時間に正確な答えをだすことができます。




