
第764回 共学中の入試問題 数の性質 5
「第764回 共学中の入試問題 数の性質 5」
これまで、近年に共学中の入試で出された「数の性質」の問題について考えています。
「数の性質」の最後となる今回は「数の性質の応用問題」を見ていきます。
1問目は、倍数と数作りの融合問題です。
【問題】100から999までの3桁の整数について、次の条件になるような3桁の整数は何個あるか答えなさい。
(1) 各位の和が「3の倍数」
(2) 各位の積が「3桁の奇数」
(3) 各位の和が「3の倍数」、または各位の積が「3桁の奇数」
(広尾学園中学校 第1回 2025年 問題2)
【考え方】
(1)
「各位の和が3の倍数」となる整数は、その数自身が3の倍数です。
99÷3=33 → 1以上99以下の3の倍数の個数は33個です。
999÷3=333 → 1以上999以下の3の倍数の個数は333個です。
333個-33個=300個
答え 300個
(2)
「各位の積が奇数」となる整数は、その数の各位の数が奇数です。
ですから、「各位の積が3桁の奇数になる」ような3つの数の組は、(3、5、7)、(3、5、9)、(3、7、7)、(3、7、9)、(3、9、9)の5組と3つの奇数がどれも5以上の組です。
(3、5、7)… 3通り×2通り×1通り → 6個
(3、5、9)… 3通り×2通り×1通り → 6個
(3、7、7)… 3個
(3、7、9)… 3通り×2通り×1通り → 6個
(3、9、9)… 3個
各位の数が5以上の奇数の場合 … 3通り×3通り×3通り → 27個
6個×3+3個×2+27個=51個
答え 51個
(3)
「各位の和が3の倍数、または、各位の積が3桁の奇数」となる部分(赤色部分)は、(1)で求めた「各位の和が3の倍数」となる整数と(2)で求めた「各位の積が3桁の奇数」となる整数の合計から、重なる部分(水色部分)を引くと求められます。
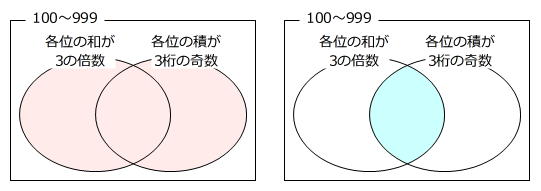
(2)で見つけた組のうち、3の倍数になる組=3つの数の和が3の倍数である組は(3、5、7)、(3、9、9)、(5、5、5)、(5、7、9)、(7、7、7)、(9、9、9)の6組です。
(3、5、7)… 3通り×2通り×1通り → 6個
(3、9、9)… 3個
(5、5、5)… 1個
(5、7、9)… 3通り×2通り×1通り → 6個
(7、7、7)… 1個
(9、9、9)… 1個
6個×2+3個+1個×3=18個 … 水色部分
300個+51個-18個=333個
答え 333個
本問は、3の倍数や奇数の特徴と作ることができる数の個数の応用問題です。
正解できないようでしたら、「倍数判定法」と呼ばれる倍数の見つけ方の問題や場合の数の考え方を利用した「作れる数の個数」の問題で基本を復習します。
2問目は、十進法と規則性の融合問題です。
【問題】0、1、2、…、9のいずれかの数字がかかれた白いカードと黒いカードがたくさんある。これらのカードを、下の図のように黒い0のカードから順に置いていく。

(1) 初めて置かれる黒い7のカードは何番目ですか。
(2) カードが (黒1)(白8)(白2)(黒8) の順に初めて並んだとき、この黒い1のカードは何番目ですか。
(3) カードが(白8)(白8)(黒8)(白9) の順に初めて並んだところで、次のカードを置くのをやめた。このとき並んでいる全てのカードのうち、黒いカードにかかれた数字の合計を求めなさい。
(慶應義塾湘南藤沢中等部 2025年 問題5 問題文一部変更)
【考え方】
(1)
黒いカードの「番目」の数は、3で割ると1余る数です。
また、並んでいるカードにかかれた数字は、1から始まる整数の各位の数を1桁の整数にばらしたものです。

初めて出てくる「7」は、1桁の整数の8番目の「7」です。
8番目÷3=2あまり2 → 白いカード
2番目に出てくる「7」は、2桁の整数「17」の「7」ですから、
1桁×10個+2桁×8個=26番目
の数字です。
26番目÷3=8あまり2 → 白いカード
3番目に出てくる「7」は、2桁の整数「27」の「7」ですから、
1桁×10個+2桁×18個=46番目
の数字です。
46番目÷3=15あまり1 → 黒いカード
答え 46番目
(2)
数字が「1 8 2 8」の順に初めて並ぶのは、80台の2桁の整数 81、82、83 をばらしたときです。
「81」の「1」は
1桁×10個+2桁×72個=154番目
の数字です。
154番目÷3=51あまり1
より、「1」は黒いカードですから、条件にあてはまります。
答え 154番目
(3)
数字が「8 8 8 9」の順に初めて並ぶのは、80台の2桁の整数 88、89 をばらしたときです。
(2)より、80台の2桁の整数をばらすと、次のようになり(白8)(白8)(黒8)(白9)という条件にあてはまります。

1桁の整数「0」から「9」のうち、黒いカードは0、3、6、9の4枚です。
0+3+6+9=18
10以上19以下の整数をばらすと数字が20個並び、20以上29以下の整数をばらすと数字が20個並び、30以上39以下の整数をばらすと数字が20個並び、… のように、2桁の整数を10から10刻みに区切ってばらすと数字が20個ずつ並びますから、20個と3個の最小公倍数である60個を1セットとして書き出します。
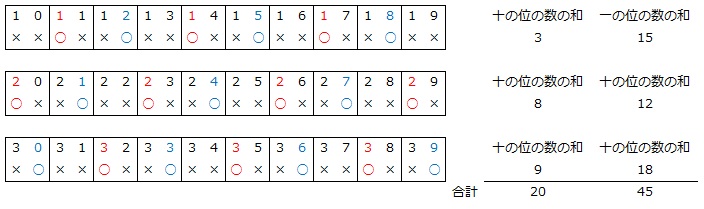
元の整数の十の位の数のうち黒いカードになる数字(赤色)の和は
3+8+9=20
元の整数の一の位の数のうち黒いカードになる数字(青色)の和は
15+12+18=45
です
40台~60台の組にある十の位の数は、10~30台の組にある十の位の数よりそれぞれ3大きいですから、その和は
20+3×10個=50
で、一の位の数は10~30台の組と同じ45です。
70台と80台の組にある十の位の数は、10台と20台の十の位の数よりそれぞれ6大きいですから、その和は
(3+6×3個)+(8+6×4個)=53
で、一の位の数の和は、10台と20台の一の位の数の和と同じ
15+12=27
です。
18+(20+45)+(50+45)+(53+27)=258
答え 258
本問は、十進法で表された数を位ごとに分ける「桁ばらし」と呼ばれる問題と数の規則性が組み合わさった応用問題です。
正解できないようでしたら、「桁ばらし」だけ、「数の規則性」だけの問題で解き方を確認しましょう。
3問目は、約数と数の規則性の融合問題です。
【問題】次の図のようなマスに駒を置いて、次の〈ルール〉にしたがって駒を動かしていきます。
![]()
〈ルール〉
① 駒が置かれたマスに書かれている数字の約数の個数が奇数個のときは1つ右のマスへ駒を動かす。
② 駒が置かれたマスに書かれている数字の約数の個数が偶数個のときは2つ右のマスへ駒を動かす。
例えば、初めに駒が12のマスに置かれたとき、駒は
12のマス → 14のマス → 16のマス → 17のマス → …
と動きます。
初めに1のマスに駒を置いて動かしたとき、次の問いに答えなさい。
(1) 1から20のマスのうち、駒が置かれたマスは何マスか求めなさい。
(2) 駒が100回目に置かれたマスに書かれている数字を求めなさい。ただし、初めに1のマスに駒を置いたときを1回目とします。
(3) 101から200のマスのうち、駒が置かれなかったマスに書かれている数字をすべてかけたとき、一の位から0が何個連続して並ぶか求めなさい。
(市川中学校 第1回 2025年 問題5)
【考え方】
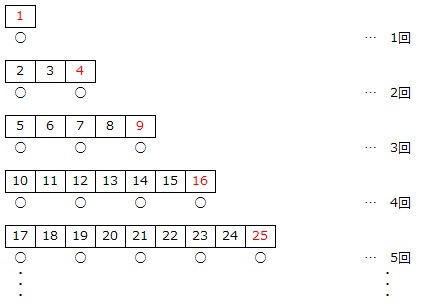
(1)
約数の個数が奇数個の整数は平方数です。
よって、駒は次のように動きます。

答え 12マス
(2)
平方数で区切って組を作ると、駒が置かれる回数は1組目は1回、2組目は2回、3組目は3回、4組目は4回、5組目は5回、… のように増えていきます。
よって、
100=1+2+3+…+13+9
より、100回目に駒が置かれるマスは14組目の9番目に駒が置かれるマスです。
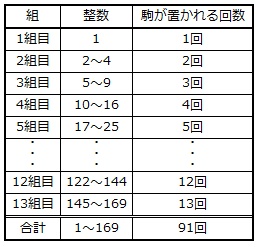
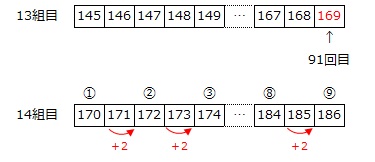
170+2×(9-1)=186
答え 186
(3)
一の位から連続する0の個数は、かけ算の式を素因数分解した形で表したときに含まれる「×2×5」の個数だけあります。
また、これまでに調べたことから駒の置かれない2の倍数の書かれたマスが5の倍数の書かれたマスよりも多くあるとわかります。
そこで、101から200までについて(2)と同じように平方数(下の赤色の数字)で区切って組を作り、駒が置かれる5の倍数が書かれたマスを調べます。
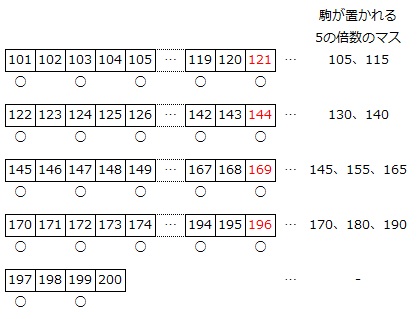
よって、101以上200以下のマスのうち、駒が置かれない5の倍数(「×5」を1個以上含む)が書かれたマスは、110、120、125、135、150、160、175、185、195、200の10マスです。
このうち、125、150、175、200の4個は「×5」を2個含む25(=5×5)の倍数、さらに125は「×5」を3個含む125(=5×5×5)の倍数ですから、一の位から連続する0の個数は
10個+4個+1個=15個
です。
答え 15個
本問は、整数と約数の個数の関係、群の中にある数の個数が増える「増殖タイプの群数列」と「末尾の0」と呼ばれる問題が組み合わさった応用問題です。
正解できないようでしたら、整数と約数の個数の関係や素因数分解を利用して解く問題、表などの規則性を見つけるための整理方法を復習しましょう。
今回は、2025年度に共学中で出された「数の性質」の応用問題をご紹介しました。
いずれもやさしい問題ではありませんので、正解できない問題があるかもしれません。
ただ、使われる考え方や整理方法、解法はどれも重要なものですので、何が課題で正解できなかったかを見つけ、補強をするようにしましょう。
![]()




