今年の1題 その10 ~女子学院中~
cherry blossoms!

お元気ですか?
ついにやってきました、桜の季節!
この淡いピンク色の花に街がつつまれると、心の中まで暖かさを感じます。
三分咲きだったとはいえ、
先日の春の「大嵐」にも花が吹き飛ばされることなかったのは、
春の息吹の力強さでしょう。
若木にも、古木にも、花が咲き誇っています。
桜の花が咲けば「入学式」ですね。
花の下を歩く、女子校生がテレビでも流れます。
ということで、今回も強引な展開からご紹介するのは女子最難関中のひとつ、
女子学院中の2012年入試問題です!
明治3年に設立された「A六番女学校」に発する伝統校で、
麹町駅と半蔵門駅の中間点、江戸城のすぐそばにあります。
「A六番」という名称は、学校のおかれた「築地居留地六番区」からきているんですね。
さてそんな伝統校であり、最難関中の入試問題ですが、
それでも新6年生ならば、十分チャレンジできます。
5年生での学習内容が、本当に中学入試にとって重要だとわかります。
【問題】
集会所に長いベンチと短いベンチと丸いすが全部で58個あります。
長いベンチに5人ずつ、短いベンチに3人ずつ、丸いすに1人ずつ座ると150人が座れます。
長いベンチに6人ずつ、短いベンチに4人ずつ、丸いすに1人ずつ座ると182人が座れます。
長いベンチは□個、短いベンチは□個、丸いすは□個あります。
「長いすの問題」といえば、「差集め算」や「過不足算」を頭に思い浮かべますよね?
では、「差集め算」や「過不足算」の整理方法を使ってみましょう。

と、ここまでくると「丸いすの個数」がわかりましたね?
いすは全部で58個ありましたから、58-32=26(個) が、丸いすの個数です。
ということは、
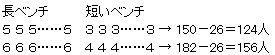
いすの個数の和=32個
とわかります。
このように「丸いす」を除いた図にすると、
⑤+3=124人
⑥+4=156人
という消去算でも、
「5人がけのベンチと3人がけのベンチが32個で124人が座れます。」という、つるかめ算でも解けます。
消去算で解くと、
たとえば、ちがいから ①+1=32
これを3倍して ③+3=96
⑤+3=124 と比べて、②=28 → ①=14 …長いベンチの個数
32-14=18(個)→短いベンチの個数
つるかめ算で解くと、
(5×32-124)÷(5-3)=18(個)→短いベンチの個数
32-18=14(個)→長いベンチの個数
となり、長いベンチ14個、短いベンチ18個、丸いす26個 が求められます。
解法自体は本当に5年生レベルですね?
ポイントは、「はじめの整理」です。
これがあったから
、「ちがいをみる → 丸いすの個数がわかる」という思考をスタートさせることができ、
3つあった変数のうちの1つがとれたことで
平易な問題になったのです。
もしこの問題に手こずるようでしたら、
①整理はできたか?
②消去算またはつるかめ算が定着しているか?
の2点から確認をしましょう。


お元気ですか?
ついにやってきました、桜の季節!
この淡いピンク色の花に街がつつまれると、心の中まで暖かさを感じます。
三分咲きだったとはいえ、
先日の春の「大嵐」にも花が吹き飛ばされることなかったのは、
春の息吹の力強さでしょう。
若木にも、古木にも、花が咲き誇っています。
桜の花が咲けば「入学式」ですね。
花の下を歩く、女子校生がテレビでも流れます。
ということで、今回も強引な展開からご紹介するのは女子最難関中のひとつ、
女子学院中の2012年入試問題です!
明治3年に設立された「A六番女学校」に発する伝統校で、
麹町駅と半蔵門駅の中間点、江戸城のすぐそばにあります。
「A六番」という名称は、学校のおかれた「築地居留地六番区」からきているんですね。
さてそんな伝統校であり、最難関中の入試問題ですが、
それでも新6年生ならば、十分チャレンジできます。
5年生での学習内容が、本当に中学入試にとって重要だとわかります。
【問題】
集会所に長いベンチと短いベンチと丸いすが全部で58個あります。
長いベンチに5人ずつ、短いベンチに3人ずつ、丸いすに1人ずつ座ると150人が座れます。
長いベンチに6人ずつ、短いベンチに4人ずつ、丸いすに1人ずつ座ると182人が座れます。
長いベンチは□個、短いベンチは□個、丸いすは□個あります。
「長いすの問題」といえば、「差集め算」や「過不足算」を頭に思い浮かべますよね?
では、「差集め算」や「過不足算」の整理方法を使ってみましょう。

と、ここまでくると「丸いすの個数」がわかりましたね?
いすは全部で58個ありましたから、58-32=26(個) が、丸いすの個数です。
ということは、
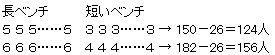
いすの個数の和=32個
とわかります。
このように「丸いす」を除いた図にすると、
⑤+3=124人
⑥+4=156人
という消去算でも、
「5人がけのベンチと3人がけのベンチが32個で124人が座れます。」という、つるかめ算でも解けます。
消去算で解くと、
たとえば、ちがいから ①+1=32
これを3倍して ③+3=96
⑤+3=124 と比べて、②=28 → ①=14 …長いベンチの個数
32-14=18(個)→短いベンチの個数
つるかめ算で解くと、
(5×32-124)÷(5-3)=18(個)→短いベンチの個数
32-18=14(個)→長いベンチの個数
となり、長いベンチ14個、短いベンチ18個、丸いす26個 が求められます。
解法自体は本当に5年生レベルですね?
ポイントは、「はじめの整理」です。
これがあったから
、「ちがいをみる → 丸いすの個数がわかる」という思考をスタートさせることができ、
3つあった変数のうちの1つがとれたことで
平易な問題になったのです。
もしこの問題に手こずるようでしたら、
①整理はできたか?
②消去算またはつるかめ算が定着しているか?
の2点から確認をしましょう。




