「第377回　2018年度 首都圏 中学入試」


東京都、神奈川県で2018年度の中学入試が一昨日の2月1日から始まりました。


昨日は、駒場東邦中、海城中などの男子難関中や、
女子御三家の桜蔭中、女子学院中、雙葉中で合格発表があり、
また、今日は、男子御三家の開成中、麻布中、武蔵中でも合格発表がありました。


今日までに第一志望の合格を獲得できた皆さんに
心よりおめでとうの言葉を贈りたいと思います。


一方、明日4日は、
聖光学院中、芝中などの第2回、
豊島岡女子中、吉祥女子中では第3回の試験が行われます。


第1回の試験で力を発揮できなかった受験生や、
惜しくも1日、2日の試験で合格を得ることができなかったお子さんにとっては、
今度こそという気持ちで今日を過ごしておられることでしょう。


明日こそこれまでの成果が発揮されんことを心より願ってやみません。




さて、今回は、2月1日に実施されました開成中の入試について見ていきます。


開成中の2018年度入試は
募集人数300名に対し、応募者数が1234名で、
2017年度の1195名、2016年度の1211名を超えるものとなりました。


では、早速、今年度の開成中の算数の問題をご紹介していきます。


始めに、「2018年度 開成中 算数」の出題範囲は以下の通りでした。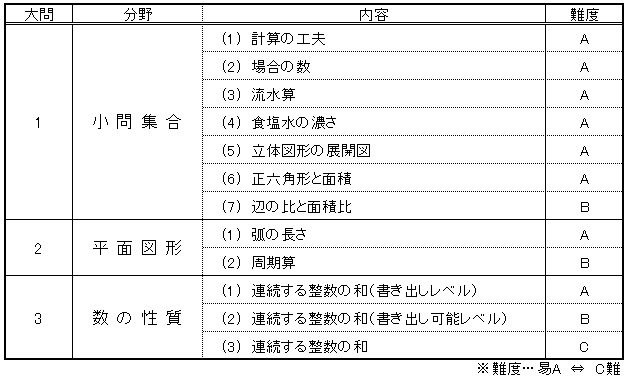




昨年2017度は、大問1の小問数は2、大問数4という構成でしたが、
今年2018年度は、大問1に全7問の小問が配置され、大問数も3となりました。


2014～2016年度も「小問集合」は0～2問でしたので、2013年度以来の形式です。


しかし、大問1の各小問は、
(1)の「□には同じ数が入ります」という
過去にも出題されたパターンの計算問題のように、
開成中受験者にとっては決して難しい問題ではありませんでしたから、
むしろ大問1を解く過程で落ち着くことができたかも知れません。




では、実際の問題を見ていきます。




2018年度　開成中　入試問題　算数より　

問題3　正方形のマスの中に、1は1個、2は2個、3は3個のように整数ｎはｎ個使い、ある整数から連続した3種類以上の整数を図のように小さい順に並べます。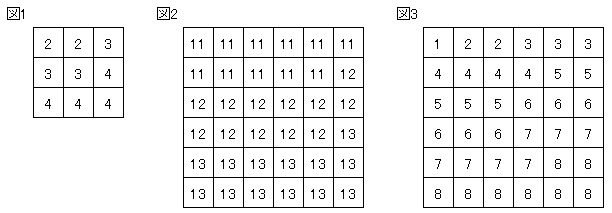



図1では3マス四方の正方形に、2を2個、3を3個、4を4個、ちょうど並べきりました。図2、図3では、6マス四方の正方形に11から13まで、1から8までの整数をちょうど並べきりました。（6マス四方に並べる並べ方はこの2通り以外ありません。）次の問いに答えなさい。(1)、(2)では、2通り以上の並べ方がある場合は、すべて答えること。解答らんには、図1の3マス四方なら［2～4］、]図2、図3の6マス四方なら［11～13　1～8］のように書きなさい。

(1)　7マス四方の正方形にちょうど並べきるには、いくつからいくつまでの整数を並べればよいですか。

(2)　10マス四方の正方形にちょうど並べきるには、いくつからいくつまでの整数を並べればよいですか。

(3)　30マス四方の正方形にちょうど並べきる並べ方は何通りありますか。また、それぞれの並べ方は何種類の整数を使うか求めなさい。(6マス四方の正方形にちょうど並べきる並べ方は図2、図3の「11～13｣、｢1～8｣の2通りです。この場合には、［2］通りの並べ方があり、それぞれ［3、8］種類の整数を使う｣と答えること。また、種類を示す整数は小さい順に並べること。)










【解答例】
(1)　
ある整数から連続した3種類以上の整数の個数の和が49個になる場合を調べます。



答え　［4～10］




答えを求めることができましたが、
問題文中に「2通り以上の並べ方がある場合は、すべて答えること」とありますから、
上記の方法では「書き漏れ」の生じる可能性があります。


そこで(2)は別の方法で解いてみることにします。




(2)　
□＋(□＋1)＋(□＋2)＋…＋(□＋○)＝100のような式を考えます。


「3種類以上」となるように100をたし算の形で表してみると、
5種類の整数を用いる「18＋19＋20＋21＋22」と
8種類の整数を用いる「9＋10＋11＋12＋13＋14＋15＋16」の
2つが見つかります。


答え　［18～22　9～16］




さて、ここまで来ると
本問は多くの難関中受験生が練習したことのある
「ある整数を連続する整数の和に分解する問題」であったことに気づけます。


「平均×個数＝和」の利用ですね。


これを利用すれば(3)も正解が可能です。


(3)
30×30＝900ですから、
「平均×個数＝900」となるような「平均」と「個数」を探します。


①　個数が「奇数個」のとき　

個数が奇数個のときは、
「連続する整数のまん中の整数＝平均」ですから、
個数は900の約数です。

・3個のとき　
300×3個＝900なので、299～301の3種類の整数を使います。

・5個のとき　
180×5個＝900なので、178～182の5種類の整数を使います。

・9個のとき　
100×9個＝900なので、96～104の5種類の整数を使います。

・15個のとき　
60×15個＝900なので、53～67の15種類の整数を使います。

・25個のとき　
36×25個＝900なので、24～48の25種類の整数を使います。


②　個数が「偶数個」のとき　

個数が偶数個のときは
「まん中＝平均が○.5」になりますから、
「平均×2×個数＝1800」として求めていきます。


このとき、
「平均×2＝奇数」でないと「まん中＝平均が○.5」にならないことに気をつけます。


1800＝2³×3²×5²ですから、
「平均×2＝奇数」のとき、「個数＝2³×○」です


・8個のとき　
225×8個＝1800ですから平均＝112.5となり、109～116の8種類の整数を使います。

・24個のとき　
75×24個＝1800ですから平均＝37.5となり、26～49の24種類の整数を使います。

・40個のとき　
45×40個＝1800ですから平均＝22.5となり、3 ～42の40種類の整数を使います。


答え　［8］通りの並べ方があり、それぞれ［3、5、8、9、15、24、25、40］種類の整数を使う　





2018年度の開成中の算数は、
大問2に長文の初見問題が出された2017年度、
題意把握が面倒な大問1や全問正解が難しい大問4があった2016年度と比べると、
比較的取り組みやすい問題であったように思います。


新6年生は、
大問4のように「学んだどの知識が必要か」を問われても困らないよう、
「知識の源＝なぜそうなるのかという理由」まで
習得する学習がこれからもできるといいですね。