第380回 2018年度中学入試の速さ 1
「第380回 2018年度中学入試の速さ 1」
前回まで、2018年度の中学入試から平面図形の問題をご紹介してきました。
今回からは、
「知識」と「条件整理力」が必要となる「速さ」の問題について
みていこうと思います。
はじめにご紹介するのは、御三家の武蔵中の問題です。
本問は5年生のときに学んだ「比と割合」、「通過算」が
実戦レベルで使えるかを確認することができますので、
新6年生は挑戦してみてください。
2018年度 武蔵中 入試問題 算数より
問題2 おもちゃの列車を走らせる円形のコースがあります。ただし、コースの一部は長さ69cmのトンネルになっています。同じ長さの列車を何両かつなげて、このコースを走らせるときに、列車の一部または全部が見えている時間を「見える時間」と呼び、列車がトンネル内にあって、まったく見えない時間を「見えない時間」と呼ぶことにします。列車3両をつなげて走らせると、見える時間41秒と見えない時間7秒を繰り返します。また、列車を5両つなげて走らせると、見える時間は44秒になります。列車の速さは一定で、何両つなげても速さは変わりません。列車の速さは毎秒何mですか。また、列車1両の長さとコースの全長はそれぞれ何cmですか。
通過算の問題です。
速さの基本的な知識のほかに通過算に必要な知識は、
(1) 通過算は「お絵かき算」である
(2) 列車の「1点の動き」に着目する
の2つです。
これらの知識をもとにして、問題の条件を「絵」にしていきます。
コースは「円形」ですが、
何周もするわけではありませんから「直線」で表した方が条件を書きやすいでしょう。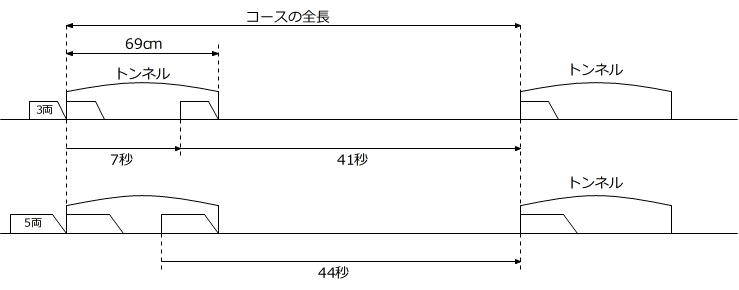
「1点の動き」については、
絵の最後の部分=コースを1周し終えたときに
「列車の最後尾とトンネルが接しています」ので、
「列車の最後尾」に着目すると、図が読み取りやすくなります。
通過算の絵は「線分図」と同じですから、
「→が表す距離」に着目します。
すると、次の2つのことが読み取れます。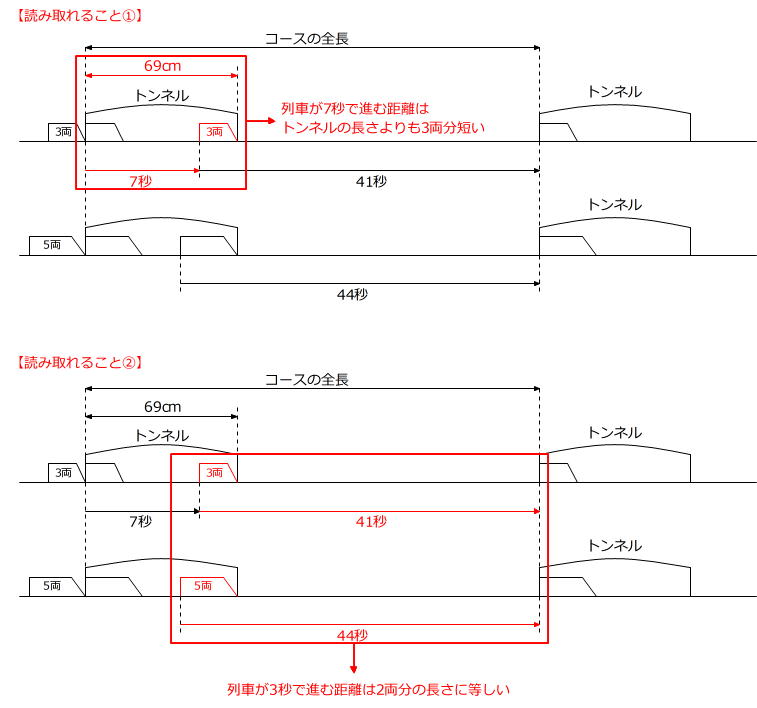
①から 列車の速さ×7秒=69cm-列車3両の長さ、
②から 列車の速さ×3秒=列車2両の長さ
とわかりますので、
(69cm-列車3両の長さ):(列車2両の長さ)=7:3 です。
この比例式を計算すると、列車1両の長さ=9cm を求めることができます。
(列車の速さ×21秒でそろえる消去算で解いてもOKです)
列車1両の長さがわかりましたので、あとは芋づる式に計算ができます。
列車の速さ=9cm×2両÷3秒=毎秒6cm
コースの全長=6cm/秒×(7秒+41秒)=288cm
通過算の基本的な解き方である
「絵を描く → 1点着目 → 矢印の表す長さ」
の通りに進めていくと、
正解を導き出せる問題でした。
もう1問、ご紹介します。
女子御三家レベルの難易度である豊島岡女子学園中の問題です。
2018年度 豊島岡女子学園中 第1回 入試問題 算数より
問題4 家と公園の間に図書館があります。AさんとBさんが家から公園までそれぞれ一定の速さで歩きます。Aさんは、家から公園まで20分かかります。Aさんが家から図書館まで歩くのにかかった時間と、Bさんが図書館から公園まで歩くのにかかった時間の合計は22分です。また、Bさんが家から図書館まで歩くのにかかった時間と、Aさんが図書館から公園まで歩くのにかかった時間の合計は23分です。このとき、次の各問いに答えなさい。![]()
(1) Bさんが家から公園まで歩くのにかかった時間は何分ですか。
(2) Aさんが家から図書館まで歩くのにかかった時間は何分ですか。
(3) AさんとBさんが家を同時に出発し、また同時にCさんが分速360mで走る車で公園を出発し家に向かいました。また、BさんはAさんとCさんが出会った地点を、AさんとCさんが出会ってから1分後に通過しました。家から公園までの距離は何kmですか。
時間条件しかありませんので、ダイヤグラムに整理します。 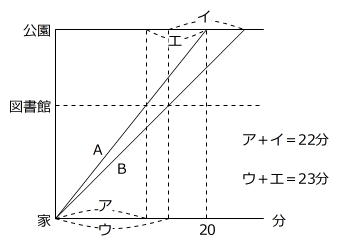
このままでも解くことはできますが、
条件が読み取りにくいと感じるようでしたら、
線分図に書き換えてみましょう。 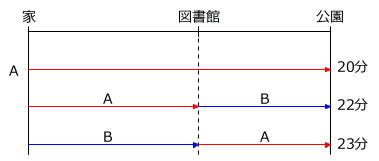
この線分図を見ると、
Bが家から公園まで歩くのにかかる時間が、
22分+23分-20分=25分 …(1)の答え とわかります。
(1)から、家から公園まで歩くのにかかる時間の比が、
A:B=20分:25分=4:5 とわかりますから、
上の線分図は次のように書き換えられます。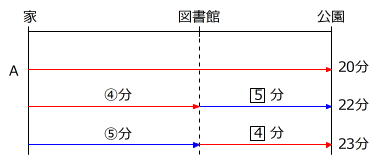
あとは消去算を使って、①分=3分、1□分=2分 が求められますので、
(2)の答えは3分×4=12分 とわかります。
(3)
線分図に表すと次のようになります。 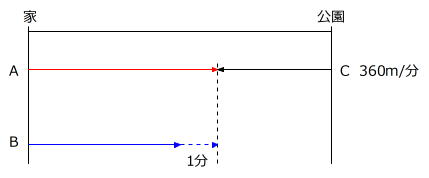
(3)はこの図から解くこともできますが、
手が止まってしまうようでしたら、
再びダイヤグラムに戻って考えてみましょう。 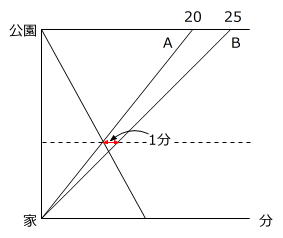
ダイヤグラムを見ると「相似」があります。 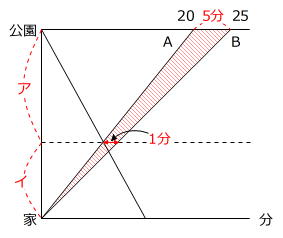
図より、ア:イ=4:1 なので、
Aは出発して4分後にCと出会ったことがわかります。
360m/分×4分×5/4=1800m=1.8km
(3)は線分図から解くこともできますし、
「時間条件が多いときはダイヤグラムに整理する」
という原則に従えば、正解も難しくはないでしょう。
今回ご紹介した2問は、
武蔵中の問題は「速さ+比例式(または消去算)」、
豊島岡女子学園中の問題も前半は「速さ+消去算」のように、
「速さの3公式」や「速さと比の関係」の知識だけでなく、
条件整理を通して「比例式」や「消去算」を用いて解く問題でした。
「知識+条件整理力」が問われる問題は今後も出され続けるでしょうから、
「速さの3公式」や「速さと比の関係」、
「旅人算・通過算・流水算・時計算の基本」がマスターできたら、
線分図やダイヤグラムの書き方、読み取り方を強化して、
難関中の問題でも正解できるようになれるといいですね。




