第430回 2019年度 中学入試 5
「第430回 2019年度 中学入試 5」
2019年度の中学入試も、ほぼすべての日程を終えようとしています。
ここまで行われた今年度の入試を見てみますと、2020年度の大学入試改革を意識してか、従来の答えを出すまでの過程を書かせる問題の他、理由などを記述する問題も出されています。
今回からは東京都、神奈川県の中学入試問題をご紹介していく予定ですが、東京都の男子御三家、開成中学でも、大問4に理由記述の問題がありました。
その開成中学の2019年度の入試状況は、出願者数が1231名、受験者数が1159名、合格者数が396名、実質倍率2.9倍とほぼ平年通り、また算数の入試問題も大問4題の構成で、出題数、難度とも平年並みといえるものでした。 
それでは、2019年度の開成中学の入試問題をいくつかご紹介していきます。
はじめは「速さと比」を学んでいれば新6年生でもチャレンジができる問題です。
2019年度 開成中学校 入試問題 算数より
大問1
K君は、自宅からおばさんの家まで、スイカ2つを1人で運ぶつもりでした。ところが、弟のS君が「ぼくも手伝う!」と言ったので、次のようにしました。
1)K君とS君がそれぞれスイカを1つずつ持って、同時に自宅を出発する。
2)K君の方がS君よりも速さが速いので、おばさんの家に先に着く。そこで、すぐにスイカを置いて、S君に出会うまで引き返す。
3)K君は、S君に出会ったらすぐにスイカを受け取り、すぐにおばさんの家に向かう。
ここで、K君の速さは
スイカを2つ持っているときは毎分60m、
スイカを1つ持っているときは毎分80m、
スイカを持っていないときは毎分100m
です。
スイカを2つ運び終えたK君がおばさんの家で休んでいると、後から追いかけてきたS君が到着しました。
S君「おにいちゃん、ぼく、役に立った?」
K君「もちろんだよ!ぼくが一人で運ぶつもりだったけど、そうするのに比べて、15/16倍の時間で運び終えられたからね。ありがとう!」
S君「ほんと?! よかった!」
次の問いに答えなさい。
(1) K君が一度目におばさんの家に着いてから、二度目におばさんの家に着くまでの時間は、K君がはじめに一人でスイカ2つを運ぶのにかかると考えていた時間の何倍ですか。
(2) 引き返したK君がS君に出会った地点から、おばさんの家までの距離は、自宅からおばさんの家までの距離の何倍ですか。
(3) S君がスイカ1つを持って進む速さは毎分何mですか。
【解答例】
時間の条件だけが与えられていますから、ダイヤグラムに整理してみます。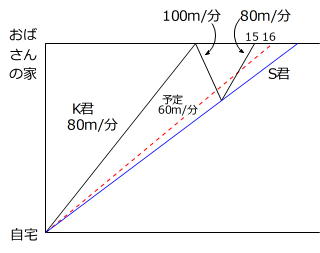
注:(3)を解くとS君は60m/分よりも速いことがわかりますが、この段階ではS君の速さが不明なので、一番遅いものとしてグラフを作成します。
(1)
速さの比80m/分:60m/分=4:3 → 時間の比③:④ 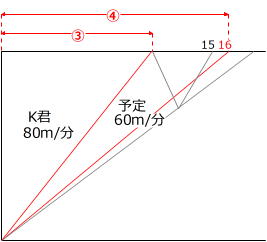
上のグラフより、K君が一度目におばさんの家に着くまでの時間は、16×3/4=12 ですから、K君が一度目におばさんの家に着いてから、二度目におばさんの家に着くまでの時間は、15-12=3です。
答え 3/16倍
(2)
(1)を利用すると、次のようになります。 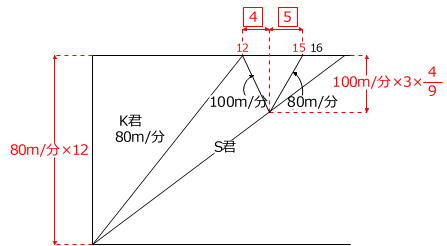
80m/分×12:100m/分×4/3=36:5
答え 5/36倍
(3)
(2)を利用します。 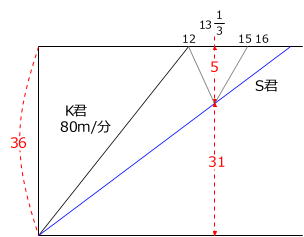
上のグラフより、K君(80m/分)とS君の速さの比は、36÷12:31÷40/3=40:31なので、S君の速さは、80m/分×31/40=62m/分です。
問題文が会話調であるためとても読みやすく、緊張している受験生にとっては「緊張感を和らげてくれる1問」だったのではないかと思います。
しかし、(1)の正解→(2)の正解→(3)の正解となる「芋づる式」の問題でしたので、得点差が生まれやすい問題でもありました。
では、もう1問、今度は立体図形の問題です。
大問2
次の図のような直方体ABCD-EFGHがあります。また、辺CD、EF、GC上にそれぞれ点P、Q、Rがあり、DP=8cm、PC=12cm、EQ=4cm、CR=9cmが成り立っています。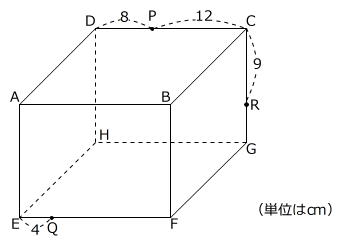
3点P、Q、Rを通る平面でこの直方体を切断し、切断したときにできる切り口の図形をXとします。
図形Xを前から見ると(面ABFEに垂直な方向から見ると)、面積が228cm2の図形に見えます。
図形Xを上から見ると(面ABCDに垂直な方向から見ると)、面積が266cm2の図形に見えます。 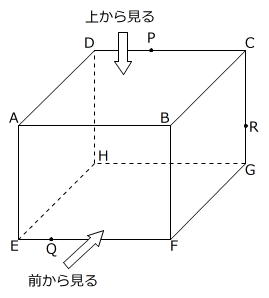
このとき、次の問いに答えなさい。
(1)図形Xは何角形ですか。
(2)直方体の高さ(辺AEの長さ)は何cmですか。
(3)直方体の奥行き(辺ADの長さ)は何cmですか。
【解答例】
(1)
切断の3原則にそって作図をします。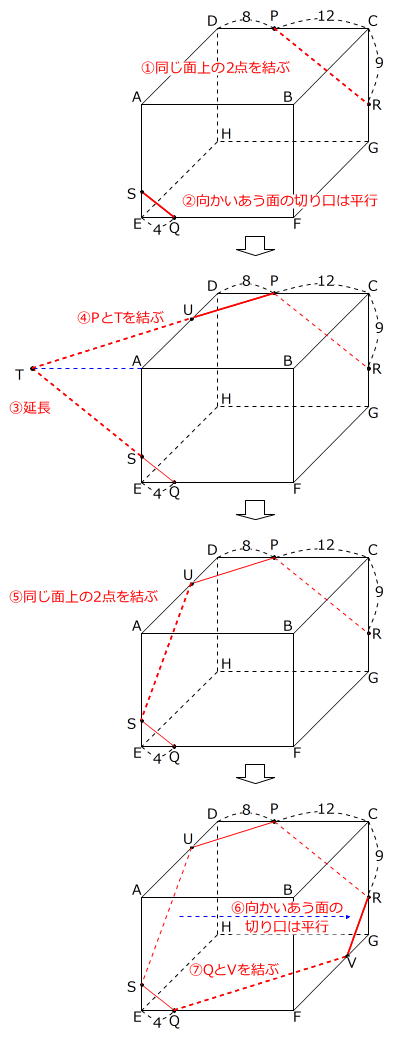
答え 六角形
(2)
(1)の作図において、求められる長さを記入します。 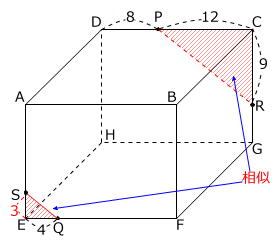
次に「図形Xを前から見た図」に値を記入します。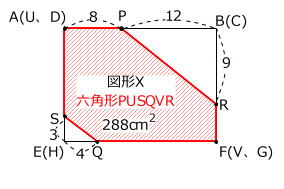
4cm×3cm×1/2+12cm×9cm×1/2+228cm2=288cm2 … 長方形AEFBの面積
288cm2÷(8cm+12cm)=14.4cm
(3)
(2)と同様に、「図形Xを上から見た図」に値を記入します。 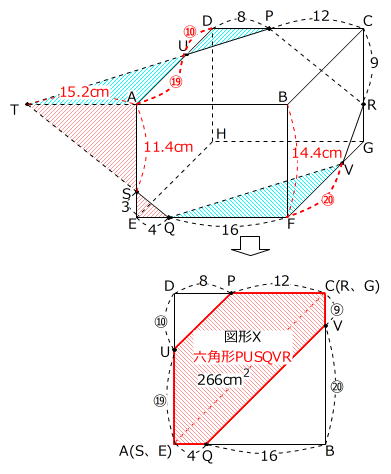
隣辺比を利用すると、三角形DUPの面積:三角形DACの面積=⑩×8:㉙×20=4:29なので、三角形QBVの面積:三角形BCAの面積=4×22:29=16:29です。
従って、長方形ABCDの面積:図形X=58:38=29:19となるので、
266cm2×29/19=406cm2 … 長方形ABCDの面積
より、
406cm2÷(8cm+12cm)=20.3cm
本問のように切断された立体図形を投影する問題は、開成中学の過去問にもありますから、(1)(2)は「受験生にとって取り組みやすい問題」だったかも知れません。
前々回にご紹介した灘中学の2019年度の入試問題も、過去問と同じ考え方を使うことのできる問題がありましたが、開成中学でも同様の出題となっています。
このように、塾の教材や過去問演習を通して、解き方や考え方を「正しく理解する」ことは、中学受験の勉強でとても大切であることがわかります。
ですから、この2月から学ぶ内容について「宿題をするだけ」や「解くだけ」ではない家庭学習に取り組み、夏休み前後から始まる志望校別の勉強で解き方や考え方を「正しく理解する」ことにつなげることができればいいなと思います。




