「第497回　合否を分ける問題の解き方 図形の回転移動 2」


前回は、中学入試の合否を分ける問題の中から「直線上を転がる四角形」について見ました。


そこから図形の回転移動の問題のポイントは、正確な作図にあることがわかりました。


今回は、前回よりもさらに作図が難しい「円の内側にそって転がる三角形や四角形」の問題について考えてみようと思います。


出題校は神奈川県の男子御三家、栄光学園中学校です。






2019年度　栄光学園中学校　入試問題　算数より　

問題1　次の問に答えなさい。ただし、円周率は3.14とします。

(1)　半径10cmの円の内部に1辺の長さが10cmの正三角形ABCが図1のようにあります。点Aをつけたまま、点Bが円周につくまで、正三角形を回転させます（図2）。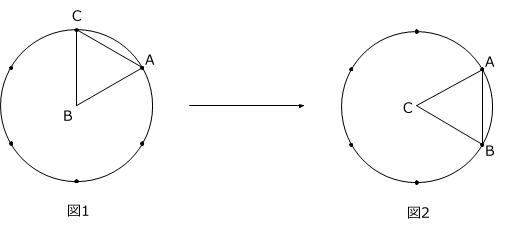



次に点Bをつけたまま、点Cが円周につくまで回転させます。このような回転を同じ向きに繰り返していきます。図1の位置からもとの位置に戻ってくるまで回転を6回繰り返したとき、点Bの動いた道すじの長さを、四捨五入して小数第2位まで求めなさい。

(2)　半径10cmの円の内部に1辺の長さが10cmの正方形ABCDが図3のようにあります。点Aをつけたまま、点Bが円周につくまで、正方形を回転させます（図4）。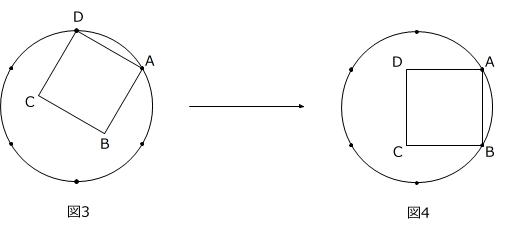



(1)と同じように図3の位置からもとの位置に戻ってくるまで回転を6回繰り返します(点A～Dの位置は元に戻るとは限りません)。点Bの動いた道すじの長さを、四捨五入して小数第2位まで求めなさい。ただし、この正方形の対角線の長さは14.1cmとします。途中の式も書きなさい。








【解答例】
(1)
与えられた図の中に、点Bの動きをかいてみます。


このとき、点Aが円の中心になっていることに気をつけましょう。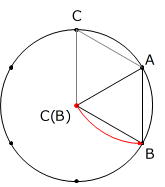




ところで、円の半径と1辺の長さが同じ正三角形は、円の中にピッタリ6個はいります。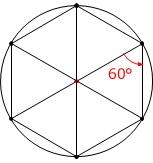




ですから、上の図より、1回に回転する角の大きさは60°であるとわかります。


さらに2回目、3回目の回転をかいていきます。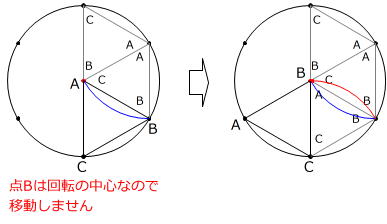




上の図のように、3回の回転で正三角形ABCは初めの位置（図1）と同じように、頂点Bが円の中心と重なりましたから、残り3回の回転は、はじめ3回の回転と同じ動きをすることになります。


ですから、点Bが動いた道すじの長さは、

20cm×3.14×1/6×2回×2周期＝41.866…　→　41.87cm

と求められます。




この問題では、回転の様子がわかるように図1、2が与えられていましたから、正確な作図は難しくないでしょう。


また、「3回の回転が1周期」ということに気づけば、計算も簡単にできますし、試験時間を節約することもできます。






ところで、円周にそって図形が転がる問題は、「直線上を転がる　→　直線を曲げて円にする」という手順で考えることもできます。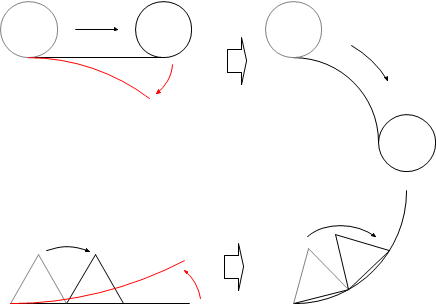




上図(下)のように、直線上を回転する場合と円周にそって回転する場合では、「回転する角度は異なります」が「回転の中心の移り変わる順序は同じ」です。


本問では、回転の中心がA→B→C→A→B→Cと移り変わっていきますから、点Bは3回に1回の割合で回転の中心となって動かないことがわかります。


つまり、6回の回転のうち、

6回×2/3＝4回

だけ点Bは回転することになります。


このことを利用すると、点Bが動いた道すじの長さは、

20cm×3.14×1/6×4回

という式でも求めることができます。




(2)
(1)の解答例の後半で見た「直線上を転がる　→　直線を曲げて円にする」という考え方を利用してみましょう。

(2)でも回転の中心はA→B→C→D→A→Bと移り変わりますから、点Bは6回の回転のうち回転の中心になることが2回あります。


1回に回転する角度は、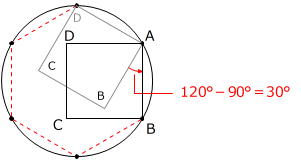



のように30°です。


ただし、(1)の「図1→図2」では点Bも点Cも回転の半径は10cmですが、(2)の「図3→図4」では、点Bと点Dの回転の半径は10cm、点Cの回転の半径は正方形ABCDの対角線となっていることに注意が必要です。


点Bの場合、点Dが回転の中心となっているとき、回転の半径が正方形ABCDの対角線14.1cmになります。


点Dが回転の中心となる回数が1回ありますから、点Bが動いた道すじの長さは、

20cm×3.14×1/12×3回＋28.2cm×3.14×1/12×1回＝23.079　→　23.08cm

と計算できます。






本問の(2)は、正確な作図は難しいのですが、「直線上を転がる　→　直線を曲げて円にする」という考え方を利用すると、問題で与えられた図を使うだけで答えを得ることができます。


ただし、「動く道すじをかきなさい」という問題も中学入試にはありますから、回転の中心の移り変わる順序に従って、点Bの動いた道すじを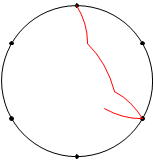



のように作図できるようになっておくことは大切です。


その上で、「直線上を転がる　→　直線を曲げて円にする」という考え方を身につけて、限られた試験時間でも正解が得られるように、これからの学習ができればいいなと思います。