第405回 夏期講習のあとの実力テスト対策 2
「第405回 夏期講習のあとの実力テスト対策 2」
お盆も終り、夏休みもあと少しとなりました。
8月中に始業式が行われる小学校もあるため、大手進学塾の夏期講習も多くは来週でほぼ終りとなります。
そして、その後にあるのが、これまでにもご紹介した様々な実力テストです。
前回は、サピックスの「6年 8月度 マンスリー実力テスト」について、夏期講習の内容とテストの出題範囲の関係、テストまでに取り組んでおきたいことを考えました。
そこで、今回は、9月2日実施予定の「四谷大塚 5年 第5回 公開組分けテスト」について見ていこうと思います。
というのも、今回の5年生の公開組分けテストは、これまでに行われた過去4回分の公開組分けテストとは少し異なる点があるからです。
次の表は、四谷大塚で行われる公開組分けテストの年間予定表です。 
この表からもわかるように、「四谷大塚 5年 第5回 公開組分けテスト」だけ、夏期講習の総復習の意味があるのでしょうか、出題範囲が「これまでに学習したすべての内容」と広範囲になっているのです。
それでは、実際にどのような出題範囲であったのかを過年度の公開組分けテストから見てみましょう。 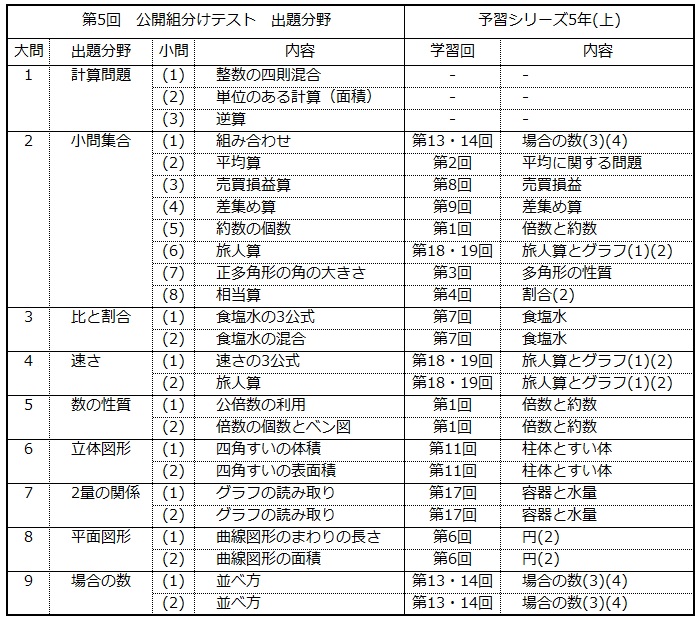
このように、「四谷大塚 5年 第5回 公開組分けテスト」は、四谷大塚がホームページ上に公開している出題範囲のとおり、第1回から第20回までの全範囲から問題が出されています。
※予習シリーズ(上)5年の第5・10・15・20回は、それぞれ直前4回分の総合回です。
では、問題のレベルはどうなっているのでしょうか。
第1回から第4回までの公開組分けテストと第5回の公開組分けテストで比較してみましょう。
まずは、小問集合についてです。
第2回 公開組分けテスト より
大問2-(4) 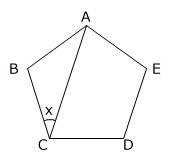 右の図の五角形ABCDEは正五角形です。角xの大きさは何度ですか。
右の図の五角形ABCDEは正五角形です。角xの大きさは何度ですか。
第5回 公開組分けテスト より
大問2-(7) 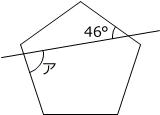 右の図は、正五角形と1本の直線をかいたものです。角アの大きさは何度ですか。
右の図は、正五角形と1本の直線をかいたものです。角アの大きさは何度ですか。
【解答例】
第2回 公開組分けテスト
大問2-(4)
正五角形の1つの外角の大きさは、360°÷5=72°なので、72°÷2=36°
第5回 公開組分けテスト
大問2-(7)
正五角形の1つの内角の大きさは、180°-360°÷5=108°なので、360°-(46°+108°×2)=98° → 180°-98°=82°
どちらの問題も、正多角形の内角や外角の大きさを求める「公式」を覚えていれば解くことができますから、問題のレベルはほぼ同じといえそうです。
もう1問、小問集合の問題を比べてみましょう。
「速さ」の問題です。
第4回 公開組分けテスト より
大問2-(8)
太郞君はA地点、花子さんはB地点を同時に出発し、それぞれ一定の速さでAB間を何度も往復します。2人はA地点とB地点のまん中からB地点に150mよったところではじめてすれちがい、その24分後に再びすれちがいました。太郞君は分速100mで進んだものとすると、花子さんの速さは分速何mですか。
第5回 公開組分けテスト より
大問2-(6) 夏子さんと秋子さんは同時に学校を出発し、夏子さんは分速65m、秋子さんは分速75mで学校と公園の間をそれぞれ1往復したところ、2人は出発してから15分後に出会いました。学校と公園の間の道のりは何mですか。
【解答例】
第4回 公開組分けテスト
大問2-(8)
問題の条件を線分図に表すと次のようになります。 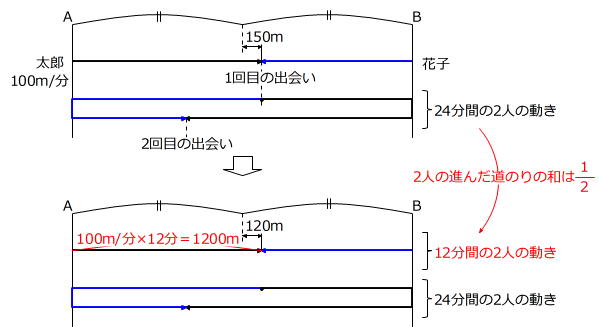
上の図のように、出発してから1回目に出会うまでの2人の道のりの和は、1回目に出会ってから2回目に出会うまでの道のりの和の半分ですから、出発してから1回目に出会うまでの時間は、24分÷2=12分です。
このとき、太郞君は100m/分×12分=1200m進んでAB間の道のりのまん中よりB地点に150mよったところで花子さんとすれちがうので、AB間は(1200m-150m)×2=2100mとなり、花子さんの進んだ道のりが2100m÷2-150m=900mとわかります。
900m÷12分=75m/分
(別解)
出発してから1回目に出会うまでに、太郞君は花子さんよりも300m多く進んでいるので、300m÷12分=25m/分が2人の速さの差です。
100m/分-25m/分=75m/分
第5回 公開組分けテスト
大問2-(6)
問題の条件を線分図に表すと次のようになります。 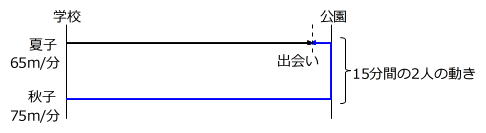
上の図から、出発してから出会うまでの2人の道のりの和は、学校と公園の間の道のりの2倍とわかります。
(65m/分+75m/分)×15分÷2=1050m
この「速さ」の問題は、テストの出題範囲が限定されている「第4回 公開組分けテスト」の方がやや難しいように感じるかもしれません。
しかし、「線分図をかいて、2人の進んだ道のりの和や差に着目する」という、往復の問題の基本パターンができていれば解ける問題ですから、問題のレベルに大きな違いはないといえるでしょう。
このように、公開組分けテストの大問2の小問集合については、夏休みの後の「第5回 公開組分けテスト」と過去4回分の公開組分けテストとで、問題のレベルに大きな違いは見られません。
ですから、夏期講習で順調に復習ができ、宿題もスムーズにこなせているようでしたら、これまで通りの学習方法で「第5回 公開組分けテスト」にも対応できると思います。
しかし、夏期講習
の宿題がうまくはかどっていないようでしたら、「第5回 公開組分けテスト」の準備をしておく必要があるといえます。
テストまでまだ2週間ほどあります。
夏期講習終了後の1週間を利用して、夏期講習教材や過去4回分の組分けテストなどから、「もう少しでマスターできそうなのだけれど…」という単元や問題を中心に、再復習ができるといいですね。




