「第406回　夏期講習のあとの実力テスト対策 3」


前回は、9月2日実施予定の「四谷大塚 5年 第5回 公開組分けテスト」について、出題範囲や前半の「小問集合」の問題レベルを確認しました。


資料となった過年度の「四谷大塚 5年 第5回 公開組分けテスト」では、四谷大塚のホームページ上に公開されているとおり、第1回から第20回まで「これまでに学習したすべての内容」がまんべんなく出されていました。


しかし、「小問集合」問題のレベルは過去4回の組分けテストとあまり変わらないものであり、夏期講習で1学期の総復習ができていればどの単元の問題も正解が可能なものでした。


そこで、今回は、後半の大問の問題レベルがどのようなものか見ていこうと思います。


1問目は「予習シリーズ5年(上)　第6回　円(2)」の範囲からの出題です。



第2回 公開組分けテスト　より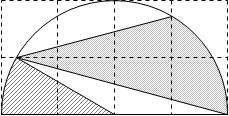　

大問9　右の図は、方眼用紙の中に半円をかき、半円の中に直線を3本ひいたものです。これについて、次の問いに答えなさい。ただし、方眼の1マスの面積は6cm²とします。（円周率＝3.14）

(1)　斜線部分の面積は何cm²ですか。

(2)　かげをつけた部分の面積は何cm²ですか。 　






第5回 公開組分けテスト　より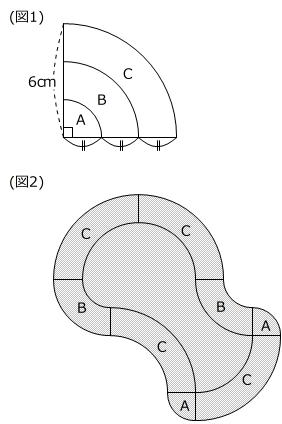　

大問8　（図1）のように、半径が6cmの四分円をA、B、Cの3つの図形に分け、これらをそれぞれいくつかならべて、（図2）のような大きな図形（かげをつけた部分）を作りました。これについて、次の問いに答えなさい。（円周率＝3.14）

(1)　かげをつけた部分のまわりの長さは何cmですか。

(2)　かげをつけた部分の面積は何cm²ですか。
















【解答例】
第2回 公開組分けテスト
大問9　
(1)　方眼1マス(＝正方形)の1辺の長さを①とします。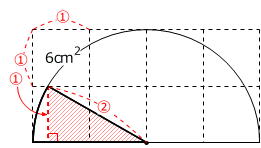




すると、上の図のように、求めるおうぎ形の中に直角三角形をつくると、高さが①で、斜辺の長さが半円の半径②に等しいことがわかりますから、求めるおうぎ形の中心角の大きさは30°です。


方眼1マスの面積が6cm² なので、①×①＝6cm² となり、
　おうぎ形の面積
＝ ② × ② × 3.14 × 1/12
＝ ( ① × 2 ) × ( ① × 2 ) × 3.14 × 1/12
＝ 6cm² × 4 × 3.14 × 1/12
＝ 6.28cm² 　が求められます。


(2)　「円問題の補助線は円周上の点と中心を結ぶ半径」という原則に従うと、次のようになります。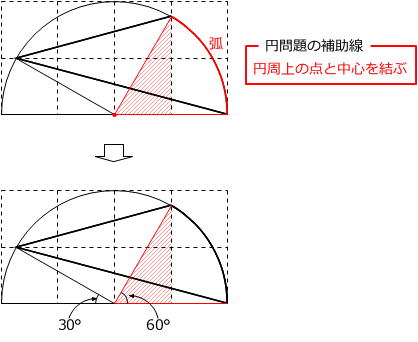




上の図より、求める図形の一部に、半径が②で、中心角の大きさが60°のおうぎ形が含まれていることがわかります。


そこで、直接面積を求めることができない図形は「まわりから引く（斜線部分＝全体－白い部分）」という求積の原則を利用すると、次のようになります。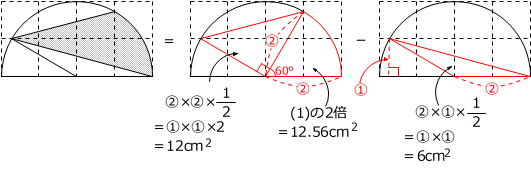





12cm² ＋ 12.56cm² － 6cm² ＝ 18.56cm²　




第5回 公開組分けテスト
大問8　
(1)　下の図のように、求める長さは、Aの弧を3つ、Bの弧を2つ、Cの弧を3つたしたものなので、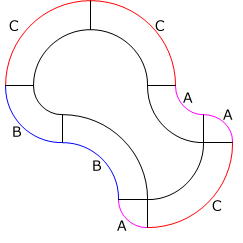




　 4cm × 3.14 × 1/4 × 3 ＋ 8cm × 3.14 × 1/4 × 2 ＋ 12cm × 3.14 × 1/4 × 3
＝ ( 3 ＋ 4 ＋ 9 ) × 3.14
＝ 50.24cm　です。


(2)　下の図のように区切ります。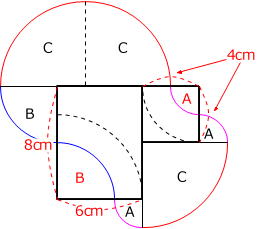




（ A2つ ＋ B1つ ＋ C3つ ＋ 48cm²の長方形 ＋ 16cm²の正方形 ）－（ A1つ＋B1つ ）
＝ 2cm × 2cm × 3.14 × 1/4 ＋ 6cm × 6cm × 3.14 × 1/4 × 3 ＋ 48cm² ＋ 16cm²
＝ 151.92cm²　

※(1)、(2)とも、相似比や面積比を用いると計算がより簡単になります。








この2問を比べると、「第2回 公開組分けテスト 大問9」が「円問題の補助線」、「30度問題」、「半径の長さがわからない円の面積（1辺×1辺の利用）」「まわりから引く」の4つの知識を利用するのに対し、「第5回 公開組分けテスト 大問8」は円周や弧の長さの公式以外、「まわりから引く」という1つの知識だけで解くことができますから、第2回の公開組分けテストの問題の方が難しいといえそうです。


しかし、公開組分けテストの最後の問題（大問9）が最上位のSコースに必要な学力があるかどうかを測定するためのものであろうことを考えると、一概に「第5回の公開組分けテストの方が易しくなっている」とはいえないでしょう。


実際、この年度の第5回の公開組分けテストの最後の問題（大問9）の「場合の数」は、同じ年度の第3回の公開組分けテストで出された「場合の数」の問題（大問6）よりもかなり難しいものでした。


これらのことから考えると、9月2日に実施される第5回の公開組分けテストには、目的に応じて2つの対策があるといえそうです。


1.　大問8までの問題で失点をしないために、夏期講習教材や過去の公開組分けテスト（大問8まで）などを利用して、知識の抜け漏れがないかを確認する。

2.　大問9での正解を増やすために、選択副教材である「週テスト問題集 5年(上)」や「応用演習問題集 5年(上)」などを利用して、大問9レベルの問題演習に取り組む。



8月中に始業式が行われる学校もあるとは思いますが、夏期講習の終わった次の1週間は比較的家庭学習の時間も作りやすいでしょうから、それぞれの目的に合わせて、上記のようなテスト対策ができるといいですね。