第408回 「速さ」の勉強方法 2
「第408回 『速さ』の勉強方法 2」
前回は、5年生が「速さ」についてどのような学習をするのかを、サピックスの5年生が9月から習う「旅人算」のA問題から見ました。
そこからわかったことは、サピックスの平常教材「Daily Support」(過年度版)のA問題は「『速さの3公式』と旅人算」という旅人算の基本が学習の中心ですが、それだけにとどまらず、線分図のかき方や使い方、仮定や比の活用についても学ぶということです。
では、B問題以降はどのような学習になるのでしょうか。
いくつか問題を見ていくことにします。
(C問題より)
東西両地間を、A、B、Cの3人が向かいあって進むことになりましたが、A、Bは東地から、Cは西地から出発しました。AとCとが出会ってから4分後にBとCが出会いました。Aは毎分100m、Bは毎分80m、Cは毎分50mとします。
(1) AとCが出会ったのは、出発してから何分後ですか。
(2) 東西両地間の距離は何mですか。
【解答例】
(1)
問題の条件を線分図に表してみましょう。
前回触れたように、線分図をかくときには2つの学習ポイントがありました。
☆学習のポイント☆
① 線分図は一気に書き上げない
② →に距離を書き込む
これらのポイントにしたがって線分図をかいていきます。 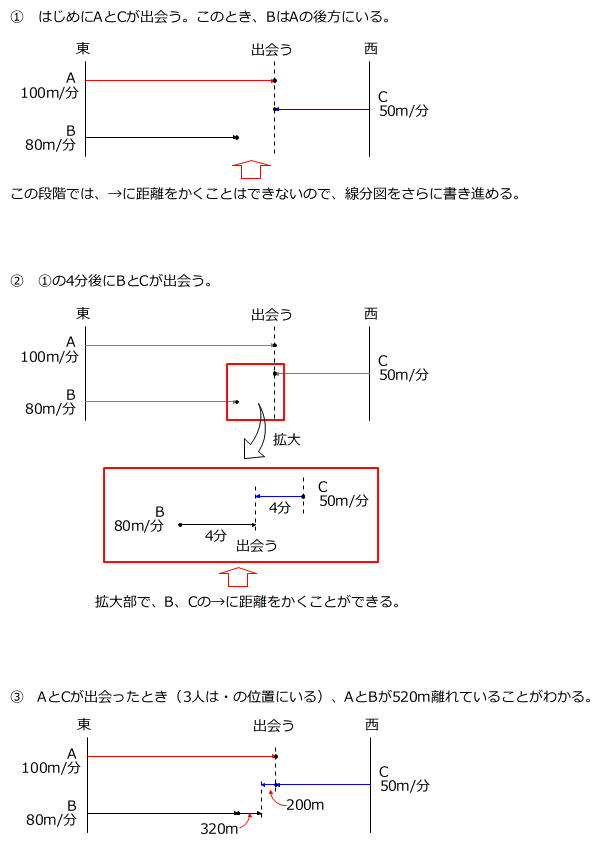
上の図から、AとCが出会ったとき(・の位置)、AはBよりも520m多く進んでいますから、旅人算の基本公式より 520m÷( 100m/分-80m/分 )=26分後 が求められます。
(2)
出発してから26分後にAとCが出会っていますから、旅人算の基本公式より ( 100m/分+50m/分 )×26分=3900m が両地間の距離です。
この問題を見ますと、「旅人算」の学習は次のような流れになっていることがわかります。 
ではC問題以降はどうでしょうか。
(D問題より)
分速100mの速さでいけば、目的地に予定の時間より1分早くつき、分速80mの速さでいけば、10分遅くつきます。目的地までの距離は何mですか。
【解答例】
この問題も条件を線分図に表してみます。 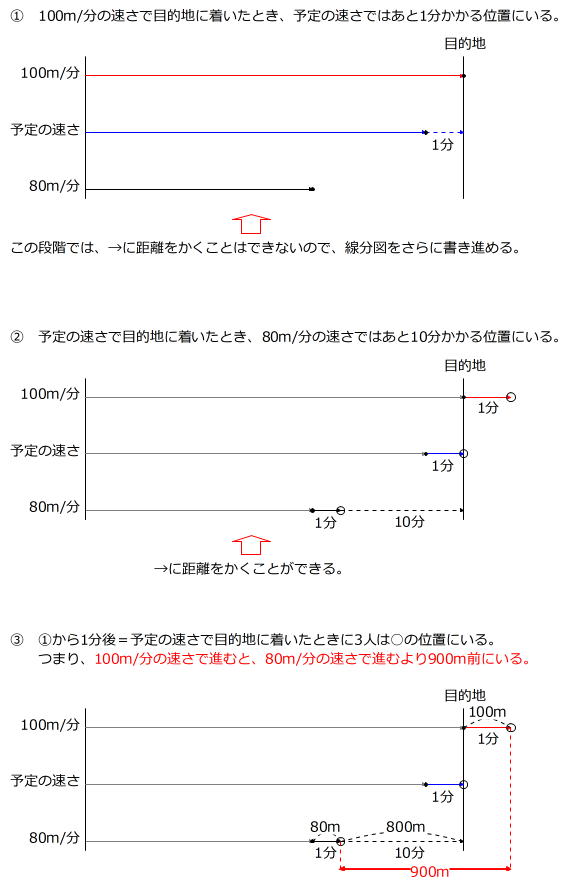
上の図から、予定の速さで目的地に着いたとき(○の位置)、100m/分で進む方が80m/分で進むよりも900m多く進んでいますので、旅人算の基本公式より 900m÷( 100m/分-80m/分 )=45分 が予定時間とわかります。
100m/分×( 45分-1分 )=4400m
上記のように線分図をかいて解いてみると、D問題のレベルがかなり高いことがわかります。
しかし、A問題で学んだ「仮定(または比)」が使えるようになっていると、この問題はより簡単に解くことができます。
【別解1】
目的地までの距離を、速さ100と80の最小公倍数400mと仮定します。
400m÷100m/分=4分
400m÷80m/分=5分
がそれぞれの所要時間ですから、距離が400mのときは目的地までの時間差は1分です。
しかし、実際の差が 1分+10分=11分 ですから、実際の距離は仮定した距離の11倍あるとわかります。
400m×11=4400m
【別解2】
目的地までの距離は100m/分のときも80m/分のときも同じですから、速さの比と時間の比は逆比になります。
速さの比 100:80=5:4
↓
時間の比 ④:⑤
⑤-④=11分 ですから、100m/分の速さで進むと ④=44分 かかることになりますので、100m/分×44分=4400m です。
これらの別解のように、①旅人算の基本公式、②線分図のかき方と使い方以外に、③仮定や比まで、A問題の学習で身につけることができれば、難しくみえるD問題も短い手順で正解することが可能です。
この後、「Daily Support」(過年度版)のE問題は3問とも「速さと比の利用」がテーマの問題となっていますので、E問題も解けることが目標であれば、「比が使える」ことは必須になってきます。
前回、今回と、5年生が「速さ」についてどのような学習をするのかを、サピックスの5年生の「Daily Support」の問題を例にみてきましたが、これらの例から、「旅人算」の学習においては、①旅人算の基本公式、②線分図のかき方や使い方、③仮定や比の3つを身につけていくことが必要だとわかりました。
次回は、「旅人算」の次に学ぶ「流水算」の勉強方法についてみていこうと思います。




