「第437回　4月に行われる大切なテスト」


春休みも半分を過ぎ、週が明ければ4月です。


4月になると、6年生にとって大切なテストが大手進学塾で行われます。


2019年度の場合、首都圏では、前回ご紹介した「志望校判定サピックスオープン」がサピックスで、「第1回合不合判定テスト」が四谷大塚でいずれも4月14日に、日能研では「実力判定テスト（全国公開模試）」が4月7日にあります。


また、関西エリアでも「公開学力テストより多少難度を高め、出題形式も多様にして、入試レベルに柔軟に対応できる」（浜学園ホームページより）「第1回 小6 合否判定学力テスト」が4月28日に浜学園で実施される予定です。


そこで、今回は、現在開講中の浜学園の春期講習の学習カリキュラムと「合否判定学力テスト」（2018年4月実施）の出題範囲を比較し、家庭学習で補完する学習単元を見てみようと思います。


浜学園の春期講習の学習カリキュラムは、次のようになっています。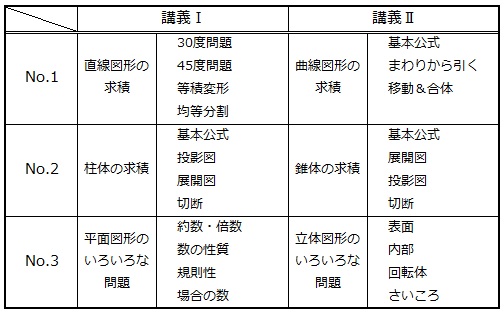




この表からわかるように、浜学園の6年生の春期講習は図形単元に特化したものとなっています。


では、「合否判定学力テスト」の出題範囲はどうでしょうか。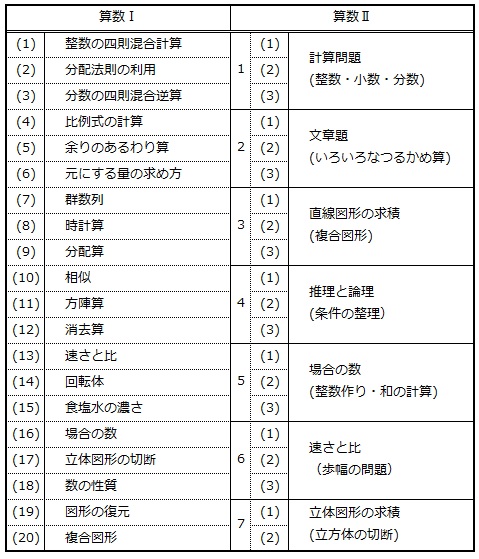




2018年の4月に実施された「合否判定学力テスト」は、他の大手進学塾のテスト同様、様々な分野からの出題となっています。


ですから、苦手な単元があれば、テストまでに家庭学習で補っておくことが必要です。


そこで、図形単元以外の問題を次に2問ご紹介いたしますので、テストに向けた準備の参考にしてみてください。






浜学園　2018年度　第1回　小6　合否判定学力テスト　算数Ⅰより　

問題(15)　A、B、C 3つの容器に食塩水が入っていて、A、B、Cそれぞれの食塩水に溶けている食塩の重さの比は3：5：11です。AとBの食塩水を混ぜるとCの食塩水と同じ濃さになり、BとCの食塩水を混ぜるとAの食塩水の2倍の濃さになります。このとき、A、B、Cの容器に入っている食塩水の重さの比は（　　：　　：　　）です。








【解答例】
食塩の重さと濃さの比が与えられていますのでこれらを整理し、「食塩の重さ÷濃さ＝食塩水の重さ」を利用して食塩水の重さを求めていきます。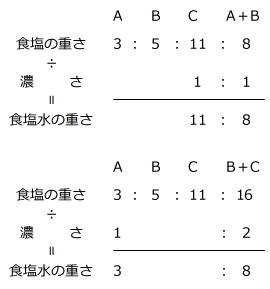




上下どちらの場合でも、食塩水の重さの和（A＋B＋C）は同じですから、連比を使用することができます。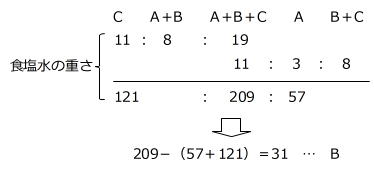




上の連比より、食塩水の重さA：B：Cは、57：31：121と求めることができます。




食塩水の濃さの単元では、食塩水の3公式「食塩水の重さ×濃さ＝食塩の重さ」や「塩分数」、面積図やてんびん法を使った問題、流れ図に整理する問題はよく練習しますが、「比の積と商」を利用する問題はそれらよりも機会が少ないため、上記のような問題の解き方を思い出せないことがあるかも知れません。


そのような場合は、5年生の塾教材の食塩水のページを開いて「比の積と商」の問題を振り返り、合わせて「続けて濃さを薄めていく問題（水入れ連発）」や「等量交換をすると同じ濃さになる問題」など解く機会の少ない問題も確認しておくとよいでしょう。






では、もう1問、今度は算数Ⅱからのご紹介です。






大問5　6枚のカード、0、1、2、3、4、5のうち、3枚を使って3けたの整数を作ります。このとき、次の問いに答えなさい。

(1)　3けたの整数はぜんぶで何個できますか。

(2)　3けたの3の倍数はぜんぶで何個できますか。

(3)　(2)でできる数をすべてたすといくつになりますか。








【解答例】
(1)
百の位の数は1、2、3、4、5のうちから1枚を選ぶので5通り、十の位の数は6枚のカードのうち百の位に使わなかった5枚のうちから1枚を選ぶので5通り、一の位の数は6枚のカードのうち百の位と十の位に使わなかった4枚のうちから1枚を選ぶので4通りですから、3けたの整数は

5×5×4＝100通り

作れます。

答え　100個　


(2)
各位の数の和が3、6、9、12になる場合を、それぞれ調べる方法もありますが、ここでは6枚のカードを「3で割った余りで分類」して解く方法を利用してみます。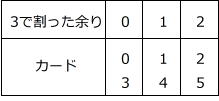




3の倍数は各位の数の和が3の倍数になる数ですから、各位の数の和を3で割った余りは0です。


ですから、3で割った余りが（0、0、0）、（0、1、2）、（1、1、1）、（2、2、2）になるようなカードを選んで3けたの整数を作ると、各位の数の和を3で割った余りは0になりますから、3の倍数を作ったことになります。


上の表を見ると、6枚のカードについて「余りが同じになる」カードは2枚ずつしかありませんから、（0、0、0）、（1、1、1）、（2、2、2）のように3枚を使う選び方はできません。


そこで、3で割った余りが（0、1、2）となるカードの組だけについて考えます。



「余り0」に0のカードを使う場合

「余り1」のカードの選び方は1、4の2通り、「余り2」のカードの選び方は2、5の2通りですから、0と他の2枚の選び方は、

1×2×2＝4通り

あります。


これらのカードの並べ方は、0のカードを百の位に使えませんので、それぞれ

2×2×1＝4通り

あります。


従って、0と他の2枚で3の倍数をつくる方法は、

4×4＝16通り

あります。


上記の計算を書き出していくと、つぎのような「カードの選び方と並べ方」になります。

0、1、2→2×2×1＝4通り
0、1、5→2×2×1＝4通り
0、4、2→2×2×1＝4通り
0、4、5→2×2×1＝4通り




「余り0」に3のカードを使う場合

「余り1」のカードの選び方は1、4の2通り、「余り2」のカードの選び方は2、5の2通りですから、3と他の2枚の選び方は、

1×2×2＝4通り

あります。


これらのカードの並べ方は、それぞれ

3×2×1＝6通り

あります。


従って、3と他の2枚で3の倍数をつくる方法は、4×6＝24通りあります。



カードの選び方と並べ方
3、1、2→3×2×1＝6通り
3、1、5→3×2×1＝6通り
3、4、2→3×2×1＝6通り
3、4、5→3×2×1＝6通り　



従って、3けたの3の倍数は、

16通り＋24通り＝40通り

あります。

答え　40個　


(3)
40個について書き出して求めることもできますが、ここでは「平均」を利用してみます。


「余り0」のカードは0、3ですから平均は1.5、「余り1」のカードは1、4ですから平均は2.5、「余り2」のカードは2、5ですから平均は3.5です。


0が百の位になる2けたの3の倍数を含めると3の倍数は全部で24通り×2＝48通りあり、平均が1.5の「余り0」のカード、平均が2.5の「余り1」のカード、平均が3.5の「余り3」のカードが、一の位、十の位、百の位にそれぞれ48個÷3種類＝16回使われますので、

｛1.5×(1＋10＋100)＋2.5×(1＋10＋100)＋3.5×(1＋10＋100)｝×(48÷3)＝13320

が48個の3の倍数の和です。




このうち、2けたの012、015、021、024、042、045、051、054の8個は問題の条件にあてはまりませんから、

12＋15＋21＋24＋42＋45＋51＋54＝264

を除いた、

13320－264＝13056

が40個の3けたの3の倍数の和です。　

答え　13056　




カードをならべて整数を作る問題では、「個数」を求める問題はよく練習しますが、「和」を「平均」で解く問題はあまりふれる機会がないと思います。


これについては、最難関中学を目指す場合は「平均」を利用することができるようになることが理想的ですが、そこまでの難問は出されない中学を目指す場合は書き出して求めることができる程度の個数の問題までが解けるようになれればよいと思いますし、3の倍数の個数についても、各位の数の和が3、6、…のように順々に調べる方法が使えればOKです。








今回は、関西エリアの浜学園で4月に行われる「合否判定学力テスト」を例に見ましたが、前回の「志望校判定サピックスオープン」と同じように、その出題範囲、レベルとも広いものとなっていました。


これらのテストまではまだ少し時間がありますので、残された春休みの期間も利用して、4月に行われる大切なテストに向けた家庭学習ができるといいですね。