「第450回　大手進学塾の夏期講習 2」


7月下旬から始まる大手進学塾の夏期講習で、志望校別対策授業を控えた6年生がどのようなことを学ぶのかを見ています。


前回は、サピックスの6年生の夏期講習教材から、第1回で学ぶ「数の性質(1)」で取り扱う問題の一部をご紹介しました。


サピックスの6年生の夏期講習のカリキュラムはこれまでに学んできた単元のほぼすべてを網羅しています。


サマーサポートの過年度版を見てみると、一度解いたことのある問題とその発展問題に加え、入試問題の類題などの新しい学習も含まれていました。


そこで、今回は同じ教材から、第3回で学ぶ「割合(1)」で取り扱う問題を見ていこうと思います。


夏期講習では割合は2回に分けられていますが、これまでに6年生の平常授業の第3回と第4回、春期講習の第1回、平常授業の第17回で学んだ年令算・倍数算・仕事算・相当算・濃さ・売買算などと、どのような関係になっているのでしょう。




実際の問題で見ていくことにします。




サピックス　夏期講習教材「サマーサポート　第3回　割合(1)」(過年度版)より　

B問題１　A君とB君の毎月もらうおこづかいの比は9：5です。今月、2人の使った金額の比は7：4で、残った金額は750円と400円でした。B君の毎月のおこづかいは何円ですか。








【解答例】
通常授業の第4回で学んだ「倍数変化算」の復習です。


倍数変化算には、線分図の利用、消去算の利用、比例式の利用などの解き方があります。


(解き方1　線分図)
問題の条件を線分図に表します。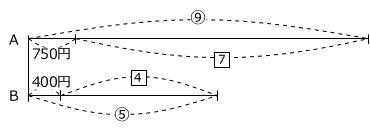




線分図の長さを9と5の最小公倍数の45 (4と7の最小公倍数の28や750円と400円の最小公倍数6000円でもOKです) にそろえます。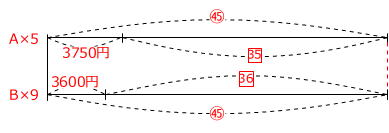




上の線分図より、１□ ＝150円とわかりますから、B君の毎月のおこづかいは、

150円×4＋400円＝1000円

です。


(解き方2　消去算)
A君とB君の毎月もらうおこづかいを⑨円、⑤円、今月、2人の使った金額を７□円、４□円とします。


問題の条件を式に表すと次のようになります。




アの式を4倍、イの式を7倍して□の値を28でそろえると、



となりますので、B君の毎月のおこづかいは、

200円×5＝1000円

です。


(解き方3　比例式)
問題の条件を整理します。




このことから、

(⑨－750円)：(⑤－400円)＝7：4

という式が作れますので、「内項の積＝外項の積」より、

(⑤－400円)×7＝(⑨－750円)×4
　↓
㉟－2800円＝㊱－3000円
　↓　
①＝200円

とわかります。


従って、B君の毎月のおこづかいは、

200円×5＝1000円

です。




この3つの解き方（「解き方1」を4と7の最小公倍数の28にそろえた場合）を見てみると、途中からの計算はどれも同じですから、自分がもっとも正解しやすい方法で、できれば時間もあまりかからない方法を選んで解ければいいと思います。




では、もう1問です。




E問題2　図書館の本の半分を整理するのに、1年生5人ですると6日間、2年生3人ですると9日間、3年生3人ですると8日間かかります。1年生5人、2年生9人、3年生4人の3学年でいっしょに図書館のすべての本を整理すると何日かかりますか。ただし。同じ学年の生徒1人あたりの1日に整理できる本の量は同じであるとします。








【解答例】
春期講習の第1回で学んだ「仕事算」の発展問題です。


仕事算には、単位あたりの仕事量を1として解く方法と、仕事全体を1（または時間の最小公倍数）にして解く方法がありますが、ここでは仕事全体を時間の最小公倍数とする方法を用いてみます。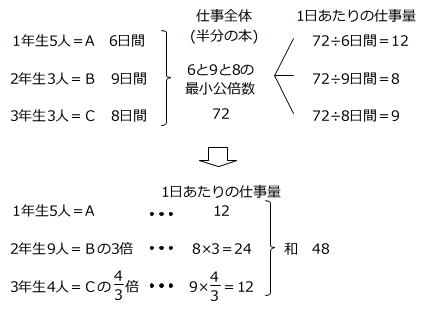




このことより、

(72×2)÷48/日＝3日

が答えとわかります。




春期講習では、仕事算を解く方法は、

「1人あたりの仕事量が同じ　→　単位あたりの仕事量＝1」、
「1人あたりの仕事量が異なる　→　仕事全体＝1（または時間の最小公倍数）」

のように、条件によって使い分けられることを学びました。


夏期講習で取り扱うこの問題では、学年によって1日あたりの仕事量が異なりますから、1年生5人をAグループ、2年生3人をBグループ、3年生3人をCグループのように「名前」をつけると、グループによって1日あたりの仕事量が異なるので「仕事全体を1（または時間の最小公倍数）」を利用して解くことができるという、春期講習の発展的な内容の問題となっていました。
（1年生1人あたりの仕事量＝12÷5人＝12/5のようにしてもOKです）








今回はサピックスの夏期講習教材「サマーサポート」(過年度版)から、6年生が夏期講習の第3回に学ぶ問題をいくつか見ました。


第3回でも、前回のようにこれまでに学んだ内容の復習から、今回はご紹介できませんでしたが難関中の入試問題の類題まで、幅広い問題が取り扱われています。


夏期講習が少しずつ近づいてきていますので、入試問題のレベルまで取り扱うクラスで夏期講習を受講する場合は、早めに既習範囲の弱点をなくしておくといいですね。