第459回 合格をするために正解したい問題 4
「第459回 合格をするために正解したい問題 4」
中学入試で合格最低点を獲得するために正解したい中級問題について、これまで「数の性質」、「比と割合の文章題」から問題を見てきました。
そこで、次の分野として今回は「速さ」について、グラフを書いて解く問題の中から選んでみます。
【問題】
2つの時計A、Bがあり、Aは正確な時刻を表しています。
時計Aが午前5時のときに、時計Bは午前5時3分
時計Aが午前11時のときに、時計Bは午前10時58分
を示していました。2つの時計の日付はすべて同じでした。この2つの時計が同じ時刻を示しだのは、この日の午前何時何分ですか。ただし、2つの時計はそれぞれ一定の割合で進んでいるものとします。
【解答例】
2つの時計の進み方を次のようなグラフに表します。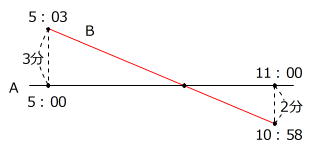
上のグラフにある、砂時計型の相似を利用します。 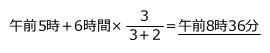
(出典:鷗友学園女子中学校 2017年度入試 第1回 問題2)
本問は「Aが進んだ時間:Bが進んだ時間」を利用して解くこともできますが、「AがBを追いこす旅人算」とみなして上のような解き方を用いると、計算が簡単になります。
では、もう1問見ていきます。
【問題】
点Pは,直線l上の点Aを出発し、毎秒1cmの速さで次のような動きをくり返します。
点Pの動き:直線l上を、まず右に5cm進み、次に左に3cm戻る。
このとき、次の問いに答えなさい。
(1) 点Pが動き始めてから20秒後には、点Pは点Aから何cm離れた点にいますか。
(2) 点Qは点Pが動き始めてから100秒後に点Aを動き始め、直線l上を毎秒1cmの速さで常に右に進みます。点Pと点Qがはじめて出会うのは、点Pが動き始めてから何秒後ですか。
【解答例】
(1)
この問題も点の進み方をグラフに表します。 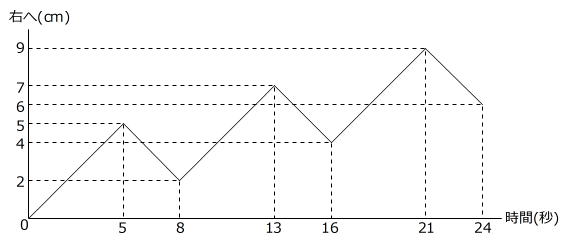
20秒後の位置は21秒後の1秒前の位置ですから、上のグラフより、9cm-1cm=8cmです。
(2)
(1)のグラフのうち「山の頂上」にあたる点を結ぶと、点Pは平均して
2cm÷8秒=0.25cm/秒
の速さで右に動いていることになります。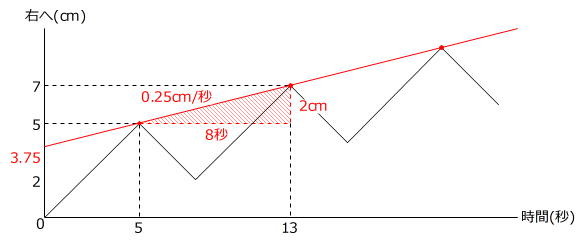
ですから点Qが動きはじめる100秒後に点Pは、
3.75cm+0.25cm/秒×100秒=28.75cm
右へ進んでいるとみなせますので、点Qは
28.75cm÷(1cm/秒-0.25cm/秒)=38秒後
に点Pに追いつくことになります。 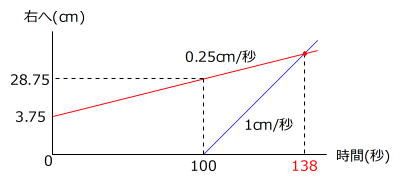
そこで、Pが動きはじめてから138秒前後のグラフを正確にかき直します。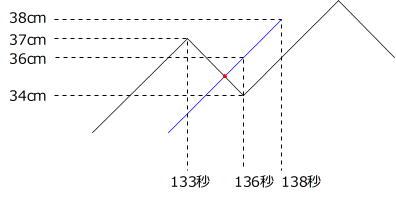
グラフの「山の頂上」にあたる点は
5秒+8秒×□
で求められますから、
5秒+8秒×16=133秒
に「山の頂上」があるとわかります。
またその位置はAから、
5cm+2cm×16=37cm
です。
上のグラフのように、点Qは点Pが動きはじめてから138秒後に38cmの位置にいますから、136秒後に点Pを2cm追いこしていることがわかります。
136秒-2cm÷(1cm/秒+1cm/秒)=135秒後
(出典:市川中学校 2018年度入試 第1回 問題3)
本問は、「カタツムリ算」と呼ばれることがある周期算の仲間です。
(1)は点Pだけの動きですから式だけで計算できますが、(2)は追いつく位置がわかりにくいですから、グラフを利用する方が解きやすいでしょう。
最後にもう1問見ていきます。
【問題】
A君とB君は地点Pから6km離れた地点Qまで走り、C君は自転車でQを出発してQP間を1往復します。3人は同時に出発し、それぞれ次のように動きます。
A君:PからQまで時速12kmで走りますが、疲れやすいので、2km走るごとに、走った時間と同じ時間だけ休みます。
B君:PからQまで一定の速さで走り続けます。
C君:Pに着いたら休まずにすぐに折り返すものとし、行きと帰りで速さは違いますが、それぞれ一定の速さで走ります。
[グラフ1]はA君がPからQまで走った様子を表しています。このとき、後の(ア)~(オ)にあてはまる数をそれぞれ求めなさい。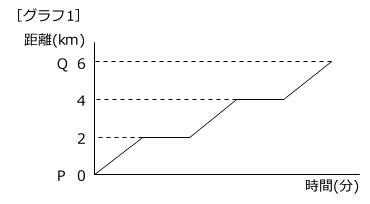
(1) A君がQに着くのは、Pを出発してから(ア)分後です。
(2) A君がB君を追い越す、または、B君がA君を追い越す回数の合計が3回のとき、B君の速さは時速(イ)km以上、時速(ウ)km未満です。
(3) B君は、A君と同時にQに着く速さで走るものとします。休んでいるA君をB君が追い越すときは2回あります。その2回のとき、C君も同時にA君が休んでいるところを通過するものとします。このとき、C君がQに戻ってくるのは、Qを出発してから(エ)分(オ)秒後になります。
【解答例】
(1)
2km÷12km/時×60=10分 10分×5=50分 → ア=50
(2)
(1)で求めた時間を[グラフ1]に書き込みます。 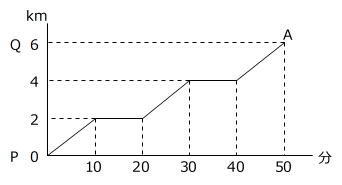
さらに「A君がB君を追い越す、または、B君がA君を追い越す回数の合計が3回」という条件を満たすように、Bの動きをグラフに書きます。
ポイントは、「追い越す回数がちょうど2回になる」、「追い越す回数がちょうど4回になる」ような2つのグラフを書くことです。 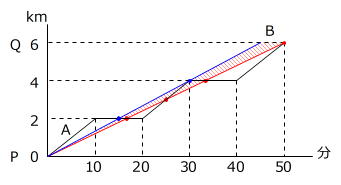
上のグラフのようにBの動きが斜線部分を通過するとき、Aを3回追い越します。
赤色のグラフより、
6km÷50/60時間=7.2km/時 → イ=7.2
青色のグラフより、
4km÷30/60時間=8km/時 → ウ=8
同じ「2回と4回」のグラフでも次のように書くと、斜線部分は「追い越しが4回」となり、不正解になりますので、注意が必要です。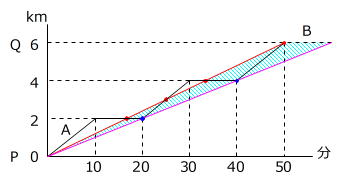
(3)
はじめにB君のグラフを記入します。 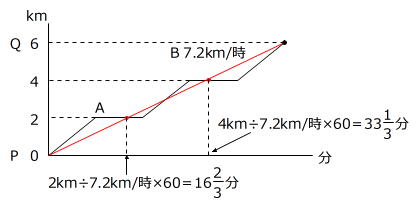
休んでいるA君をB君が追い越す位置と時刻がわかりましたから、この点を通るようにC君のグラフを書きます。 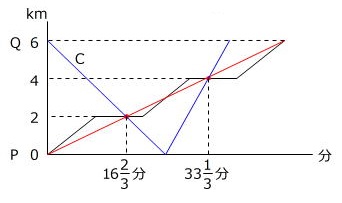
上のグラフの中にある「ピラミッド型相似」を利用すると、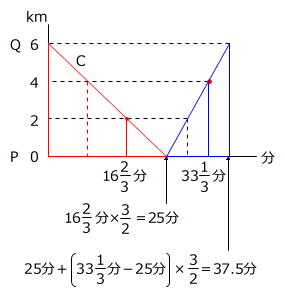
とわかります。 → エ=37、オ=30
(出典:浅野中学校 2017年度入試 問題3)
本問は(2)で「速さの範囲」を求めますので、「範囲の表示がしやすい」グラフを利用すると正解しやすくなります。
今回ご紹介した問題は、一般的なダイヤグラム(進行グラフ)の問題とは少し異なっていました。
しかし、今回の問題を解くためのグラフを書く力は一般的なダイヤグラムを書く力がベースになっています。
サピックスの場合、「グラフ」は6年生の春期講習で取り扱われるカリキュラムとなっていますので、機会があれば先行して一般的なダイヤグラム問題にふれておくと、講習会の学習もより効果的になると思います。




