第477回 中学入試で出題される「規則性」 3
「第477回 中学入試で出題される「規則性」 3」
1月になると首都圏では「1月校」の中学入試が行われ、また、関西エリアでは18日から2府4県で入試が始まります。
そこで今回は、これまでご紹介している「規則性」に関する問題を、2019年度の「1月校」入試から見てみようと思います。
1問目は、6000人を超える受験者のあった栄東中学校のA日程の入試問題からです。
2019年度 栄東中学校 A日程(四谷大塚 80%偏差値 男子57・女子59)より
問題5
直角二等辺三角形ABCがあります。1つの直角二等辺三角形に対して、直角をなす点から向かい合う辺に垂直な線を引き、三角形を分割していく操作を繰り返していきます。2本以上の線が交わってできる点を頂点とよぶとき、次の問いに答えなさい。例えば、1回目の操作の後の図形は図1で頂点の個数は4個、2回目の操作の後の図形は図2で頂点の個数は6個、3回目の操作の後の図形は図3で頂点の個数は9個です。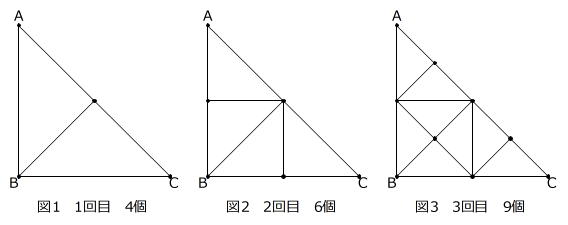
(1) 4回目の操作の後の頂点の個数を求めなさい。
(2) 5回目の操作の後の頂点の個数を求めなさい。
(3) 9回目の操作の後の頂点の個数を求めなさい。
【解答例】
(1)
実際に図を書いて調べます。 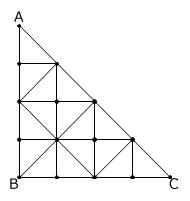
図から、15個とわかります。
(2)
(1)と同様に図を書いて調べます。 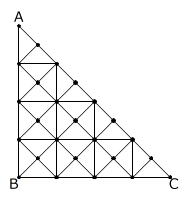
図から、25個とわかります。
(3)
ここまでは図を書いて調べることができましたが、これ以上は正確な図を書くことが難しいので、例と(1)、(2)の図から、規則性を探します。 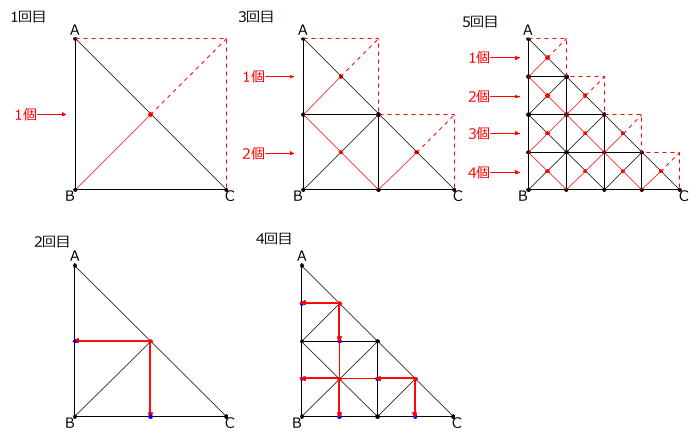
上の図のように、「奇数回目の操作」で増える頂点は正方形(赤色の点線部分を含む)の対角線の交点ですから、正方形が順に1個、1+2=3個、1+2+3+4=10個、…、とできますので、増える頂点の個数は1個、3個、10個、…です。
また、「偶数回目の操作」では、1回前の「奇数回目の操作」で増えた点の2倍だけ、頂点の個数が増えています。 
上の表より、9回目の操作の後の頂点の個数は289個と求められます。
※「平方数」を利用して答えを求める方法もあります。
本問は「図形の規則性」の問題です。
「図形の規則性」の問題で規則性が見つけにくいときは、「例示の続きの図を1つまたは2つかいてみる」と、上記のように規則が見つけやすくなります。
ではもう1問、同じく栄東中学校の東大クラス選抜Ⅰの入試問題からです。
2019年度 栄東中学校 東大クラス選抜Ⅰ(四谷大塚 80%偏差値 男子66・女子69)より
問題1-(6)
大きな円盤に、中心を通る3本の直線を引くと,円盤は6個の部分に分かれました。ここに4本目の直線を引いたとき、円盤は4個の部分が増えて10個の部分に分かれました。この後、円盤がなるべく多くの部分に分かれるように1本ずつ直線を引きます。7本目を引いたとき、円盤は( ア )個の部分が増えて( イ )個の部分に分かれました。
【解答例】
図形の問題ですが図が与えられていませんので、自分で図をかいて調べます。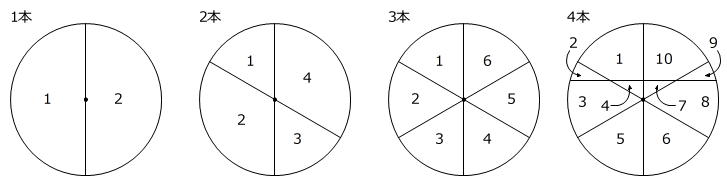
4本目まで線を引いた図を見ても規則性が見つけにくいときは、5本目の線も引いてみましょう。 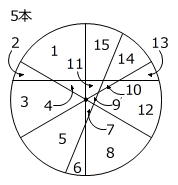
図をかいたら、わかることを表に整理します。 
この表だけでは、規則性を見つけることは難しいようですが、6本目の線を引いた図を正確にかくことも難しいので、表に項目をつけ足してみます。 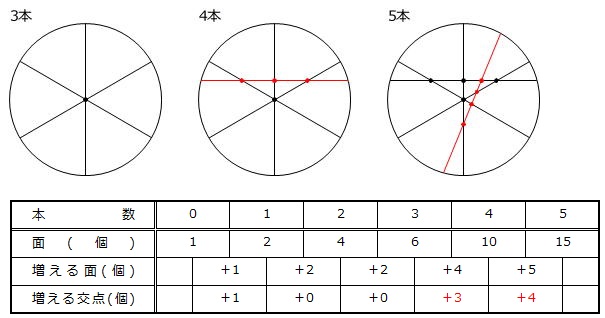
問題の条件に「なるべく多くの部分に分かれる」とありますから、書き加える線は、その図にかかれている全ての線と交わればよいことになります。
つまり、4本目の線を引くときはすでに書かれている3本の線と交わればよいので交点が3個でき、書き加えた線がその3つの交点によって4つに分けられますから、面も4個増えることになります。
同様に、5本目の線を引くときはすでに書かれている4本の線と交わればよいので交点が4個でき、書き加えた線がその4つの交点によって5つに分けられますから、面も5個増えることになります。
従って、線を7本目まで書き加えたときの表は下のようになります。
答え ア 7 、イ 28
本問は「図形の規則性」の定番の問題です。
しかし、条件を少しずつ変えることができますので、「面が増える理由」を理解しておかないと正解しそびれることになります。
このように、「図形の規則性」の問題は、初見の場合は「図を書き加えながら規則性を見つける」ことになりますし、定番の問題はその原型の問題演習のときに「規則性の理由」を学習しておくことが重要になります。
サピックスの6年生のカリキュラムでは、春期講習の第5回、通常授業の第14回で「規則性」が取り扱われます。答えを「書きだし」で求められるようになれば「規則性の理由」まで身につけて、正解できる問題を増やすことができればいいなと思います。




