第476回 中学入試で出題される「規則性」 2
「第476回 中学入試で出題される「規則性」 2」
中学入試で出された「規則性」に関する問題をご紹介しています。
前回は、「2で割ったときの余り」が利用できる「数の規則性」の問題でしたが、今回はどのような工夫ができる問題でしょうか。
さっそく問題を見ていきましょう。
2019年度 サレジオ学院中学校 A試験(四谷大塚 80%偏差値 男子60)より
問題4
次のような[規則]に従って整数の列を作ります。
[規則]
(ア) 1番目の数は1、2番目の数は1です。
(イ) 3番目以降の数は、1つ前の数と2つ前の数を足した数です。
このとき、次の問いに答えなさい。
(1) 1番目の数から10番目の数まですべて答えなさい。
(2) 1番目の数から30番目の数までに3の倍数はいくつありますか。
(3) 上の[規則]で、(イ)はそのままで、(ア)を
(ア) 1番目の数はX、2番目の数はYです。
という規則に変えて、新しい整数の列を作ることを考えます。ただし、X、Yには、それぞれ4から9までの整数のいずれかが入り、XはYよりも小さい整数とします。このとき、新しい整数の列の1番目から100番目の数の中に、3の倍数が25個あるようなX、Yの組合せをすべて答えなさい。
【解答例】
(1)
この問題の[規則]は、「フィボナッチ数列」という数列の作り方を表しています。
1番目の数 1
2番目の数 1
3番目の数 1番目の数+2番目の数=1+1=2
4番目の数 2番目の数+3番目の数=1+2=3
5番目の数 3番目の数+4番目の数=2+3=5
6番目の数 4番目の数+5番目の数=3+5=8
7番目の数 5番目の数+6番目の数=5+8=13
8番目の数 6番目の数+7番目の数=8+13=21
9番目の数 7番目の数+8番目の数=13+21=34
10番目の数 8番目の数+9番目の数=21+34=55
答え 1、1、2、3、5、8、13、21、34、55
(2)
「30番目」まで書き出して調べてもよいのですが、「調べる量が多い」ということは、「何か規則性があるのかも…?」と予測してみましょう。
そこで(1)で書き出した数列を調べてみると、次のようになります。 
上の結果より、「×××○」の4個1組が繰り返されていることがわかります。
30番目÷4個/組=7組あまり2番目 → 1個×7組+0個=7個
一応答えは求められましたが、「本当に4個1組?」という不安が残りそうです。
このように不安を感じたときは、もう少し調べる量を増やし、「大丈夫そうだ!」という安心感を持って次の問題に進むことが、テストのときは大切です。
しかし、家庭学習など時間の制約が少ないときは、次の別解のように、繰り返す「理由を考える」とよいでしょう。
(別解)
3の倍数が問題となっていますから、(1)の数列について、「3で割った余り」を調べていきます。 
前回の「学習のポイント 2で割った余りを利用した整数のたし算」と同じように、今回は「3で割った余りを利用した整数のたし算」を使います。 
問題の規則に従って、「余りについても前の2数をたす」と、上のように「8個1組」を繰り返します。
「4個1組」でも(2)の正解を得ることはできますが、実は「8個1組」という規則だったことがわかります。
30番目÷8個/組=3組あまり6番目
↓
2個×3組+1個=7個
この「8個1組」を利用すると、次の(3)も正解が可能になります。
(3)
4~9の6つの整数を3で割った余りで整理し直します。 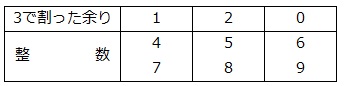
この表を利用すると、例えば、(X、Y)=(4、5)は、(X、Y)=(1、2)に置き換えることができます。
従ってX、Yの組み合わせは、3で割った余りの9つの組(0、0)、(0、1)、(0、2)、(1、0)、(1、1)、(1、2)、(2、0)、(2、1)、(2、2)を調べても同じことになります。
ところが、
(0、1)のときは3番目の数が0+1という計算になり、
(0、2)のときは3番目の数が0+2という計算になり、
(1、0)のときは3番目の数が1+0という計算になり、
・
・
・
(2、2)のときは3番目の数が2+2という計算になりますから、(0、0)以外の8つの組については、(2)の別解で見た「(余りの)2数の和」の8つの式を繰り返すことになります。
ですから、これらの8つの組の場合、できあがる数列は次のような「ループ(環状)」になることがわかります。 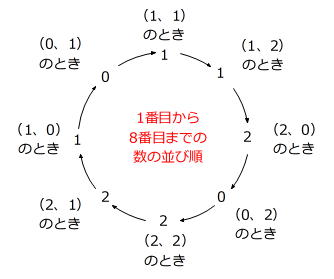
このループから、(0、0)以外の8つの組は、8個1組の中に「必ず3の倍数が2個含まれる」ことがわかり、問題は、100番目までに3の倍数が25個含まれる場合についてですから、
100番目÷8個/組=12組あまり4番目
↓
1番目から4番目までに3の倍数を1個だけ含むとき、3の倍数の個数が
2個×12組+1個=25個
となります。
ところが上のループを見ると、どこから数え初めても1番目から4番目までの4つの数の中に「0」が1個だけありますから、(0、0)以外の8つの組はこの問題の条件を満たしていることがわかります。
一方、(0、0)の組=(6、9)の組は、すべて3の倍数が並びますので、問題の条件にあてはまりません。
ですから、(3)の答えは(6、9)以外の全ての組となります。
答え (X、Y)=(4、5)、(4、6)、(4、7)、(4、8)、(4、9)、(5、6)、(5、7)、(5、8)、(5、9)、(6、7)、(6、8)、(7、8)、(7、9)、(8、9)
本問は「フィボナッチ数列」という「数列(規則的に並ぶ数)」の問題でしたが、小問(2)、(3)を解く際には、「3で割った余り」を利用しています。
このように「余り」を利用する考え方のことを「剰余類」や「剰余系」といいますが、「剰余類」は中学入試で出される「数の性質」や「数の規則性」の難しい問題で使うことがあります。
ですから、難関中を目指している場合は特に、「1、4、7、10、13、16、…は、3ずつ増える数、3で割ると1余る数、3の倍数+1、各位の数の和を3で割ると1余る数」などのように、複数の表現で数の説明ができるようになると理想的だと思います。




