「第485回　2020年度の中学入試 6」


前回から、人気が高まっている大学の付属校について、2020年度の中学入試問題をご紹介しています。


今回は、早稲田大学の系属校である早稲田中学校の第1回の入試問題を見ていこうと思います。


早稲田中学校の第1回の算数の入試問題は、2019年度と同じく大問5題という構成でした。




2020年度　早稲田中学校　入試問題　第1回　算数より　

問題1-(1)　からある数を引いて最も大きい整数にします。そのある数は何ですか。約分できない分数で答えなさい。








【解答例】
一瞬、何を問われているのか、戸惑いそうになる問題ではないでしょうか。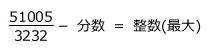



しかし、上記のような式に表すと、問題の仮分数を帯分数に直す問題であることがはっきりします。

51005÷3232＝15あまり2525

ですから、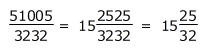



となります。 　






本問の計算は簡単ですが、「文章を正しく読む」ことができないと、「？」が頭に飛びかねない問題だったでしょう。


このようなところにも、新しい「大学入学共通テスト」で「思考力」問題が出されることが反映されているように思えます。




では、もう1問です。






問題3　三角すいABCDの頂点Aに点Pがあり、点Pは1秒ごとに他の頂点に移動します。たとえば、2秒後に点Pが頂点Aにある移動の仕方は全部で3通りです。次の問いに答えなさい。

(1)　3秒後に点Pが頂点Aにある移動の仕方は全部で何通りありますか。

(2)　4秒後に点Pが頂点Aにある移動の仕方は全部で何通りありますか。

(3)　5秒後に点Pが頂点Aにある移動の仕方は全部で何通りありますか。

(4)　9秒後に点Pが頂点Aにある移動の仕方のうち、3秒後に頂点Bにあり、6秒後に頂点Aにある移動の仕方は全部で何通りありますか。








【解答例】
各頂点への行き方が何通りあるかを1秒ごとに自分で図をかいて解く問題です。

(1)　
点Pが、1秒後、2秒後、3秒後に移動する仕方が何通りあるかを順にかいて調べます。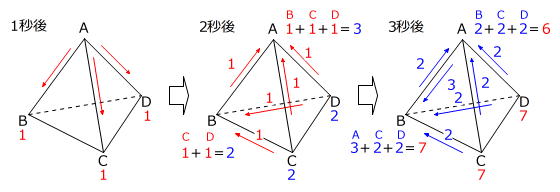



上の図より、3秒後に点Pが頂点Aにある移動の仕方は全部で6通りとわかります。

答え　6通り　


(2)
(1)の図より、点Pが3秒後から4秒後に頂点Aに移動する仕方は、頂点B、C、Dからそれぞれ7通りありますから、

7通り×3＝21通り

です。　

答え　21通り　


(3)
(1)の図より、点Pが4秒後に頂点Bに移動する仕方は、頂点Aから6通り、頂点C、Dからそれぞれ7通りありますから、

6通り＋7通り×2＝20通り

とわかります。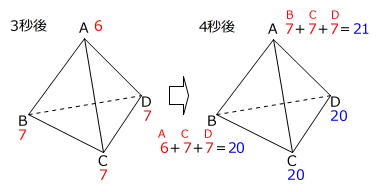




従って、点Pが5秒後に頂点Aに移動する仕方は、頂点B、C、Dからそれぞれ20通りありますから、

20通り×3＝60通り

です。　

答え　60通り　


(4)
(1)～(3)と同じように、5秒から9秒後までの図をかいて調べてもOKですし、次のように「踏み台解法」を利用して解くこともできます。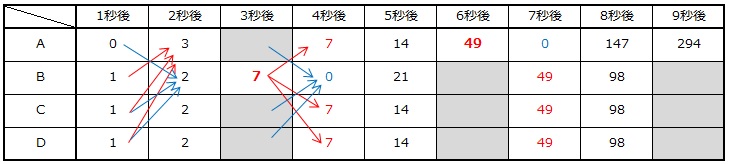



上の表より、9秒後に点Pが頂点Aにある移動の仕方のうち、3秒後に頂点Bにあり、6秒後に頂点Aにある移動の仕方は全部で294通りとわかります。

答え　294通り　

（別解）
(1)の図を利用します。


点Pが頂点Aから3秒後に頂点Bに移動する仕方は7通りです。


3秒後に点Pが頂点Bから頂点Aに6秒後に移動する仕方は、(1)で頂点Aから3秒後に頂点Bに移動する仕方と同じですから、

7通り×7通り＝49通り

です。


同様に、6秒後に点Pが頂点Aから頂点Aに9秒後に移動する仕方は、(1)で頂点Aから3秒後に頂点Aに移動する仕方と同じですから、

49通り×6通り＝294通り

のようにして求めることもできます。






本問は、「自分で図をかく」、「小問(1)～(3)を通して規則性に気づく」という点から「思考力」問題だといえそうです。


しかし、そのためには「時間ごとの道順解法（時系列のイチイチ解法）」が使いこなせることも必要ですから、「知識」も問われているといえるでしょう。






このように、「思考力」問題を解くためには、十分な「知識」とそれらを正確に使いこなせる「アウトプット力（答えまで過程を正確に処理する力）」が欠かせません。


ですから、志望校別の傾向対策が始まるまでの約半年がこの「知識」と「アウトプット力」を高める期間、9月以降が「思考力」問題対策の期間と考えて、6年生前半の学習に取り組んでいくことが望ましいと思います。