蝸牛！

お元気ですか。

雨になると活発に活動する生き物もでてきます。


このカタツムリ、
民俗学の柳田國男氏によれば、時代によって呼ばれ方が変わっているそうで、
古い順からツブリ（ツボラ）、カタツムリ、デンデンムシ（デデムシ）となり、
古い言い方であるほど、かつての都、京都から遠い地方に残っているそうです。

ちなみに和名のマイマイは東京地方の方言なんだそうです。

さて、そんなカタツムリといえば、
渦巻き模様の殻がシンボルですよね。

ということで今日も曲線図形、円とおうぎ形です。
（あいかわらず，強引！）

次の図は正方形の中に中心角が90°の2つのおうぎ形をかさねたものです。斜線部分の面積を求めしましょう。ただし、円周率は3.14です。


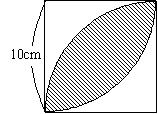
おなじみの問題ですね。

四分円（90°のおうぎ形）－直角二等辺三角形＝弓形
弓形×2＝斜線部分の面積
という解き方が一番多いでしょうか。


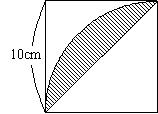
少し計算が大変ですが、
10×10×3.14÷4＝78.5
10×10÷2＝50
78.5－50＝28.5
28.5×2＝57（cm2）　です。

「重なり」というヒントに気づいたお子さんは
四分円×2－正方形＝斜線部分の面積
と解けたでしょうね。素晴らしいです！


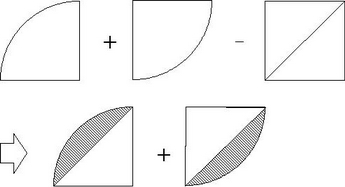
10×10×3.14÷4＝78.5
78.5×2－10×10＝（cm2）
少し計算を節約できました！

でも、
10×10×0.57＝57（cm2）
と、簡単に解いたお子さんもいるのでは？

正方形の中にぴったり入った
レンズ形（葉っぱ形、木の葉形、ラグビーボール形など様々な呼び名があります！）の面積は、
正方形の面積の0.57倍になるんです。

正確に覚えておくととても便利ですね。

でも、円周率が3.14のときだけですよ！

この3つの解き方を見比べると、
計算間違いの可能性の少なさや所要時間の少なさという点で
「0.57」を覚えておくとテストで役立ちますね。

では、もう1問。
次の図は中心角が90°の3つのおうぎ形です。斜線部分の面積を求めしましょう。ただし、円周率は3.14です。

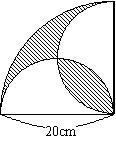
ここでのポイントは
①レンズ形は半分に切る　→　弓形ができる
②弓形は、おうぎ形－三角形　または　移動して合体
の2点です。

このポイントは他の問題でも使えるので、ぜひ覚えておきたいですね！

すると次のようになるので、


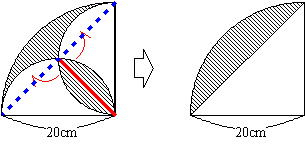
20×20×3.14÷4－20×20÷2＝114（cm2）
とわかります。
もし、下の図のアとイの面積が等しいことを知っていたら、


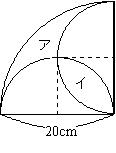
イの面積を2倍して
10×10×0.57×2＝114（cm2）
とできますね。

図形問題にはこのように「覚えておくと、お得！」というコツがたくさんあります。

また紹介していきますね。