「第７４６回　女子中の入試問題　平面図形 ４」

今回も、前回に引き続き、２０２５年度に女子中の入試で出された「平面図形」の中から「辺の比と面積比」の問題を取り扱っていきます。

１問目は「２組の相似（ダブル相似）」問題です。

【問題】図の平行四辺形ＡＢＣＤにおいて、ＡＥ：ＥＢ＝１：３、ＢＦ：ＦＣ＝１：４、ＥＨ：ＨＣ＝４：５です。次の［ア］から［ク］に当てはまる数を求めなさい。ただし、比は最も簡単な整数の比で表しなさい。

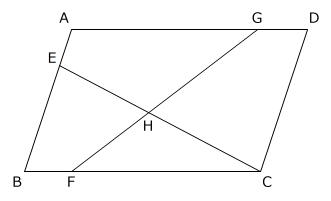
（１） ＡＧ：ＧＤを求めます。

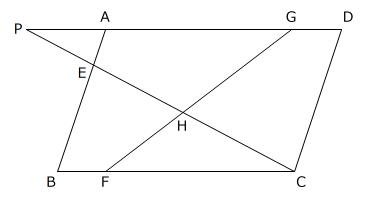
ＣＥの延長とＤＡの延長が交わる点をＰとします。ＰＡ：ＢＣ＝［ア］：［イ］です。また、ＰＧ：ＦＣ＝［ウ］：［エ］ですから、ＡＧ：ＧＤ＝［オ］：［カ］です。

（２） 四角形ＧＨＣＤの面積は平行四辺形ＡＢＣＤの面積の何倍かを求めます。

三角形ＧＣＤの面積は三角形ＡＣＤの面積の［キ］倍です。よって、四角形ＧＨＣＤの面積は平行四辺形ＡＢＣＤの面積の［ク］倍です。

（鷗友学園女子中学校　第二回　２０２５年　問題５　問題文一部変更）

【考え方】

（１）

三角形ＡＰＥと三角形ＢＣＥは相似で、

ＡＥ：ＢＥ＝１：３

ですから、

ＡＰ：ＢＣ＝ＰＥ：ＣＥ＝１：３

です。（図１）

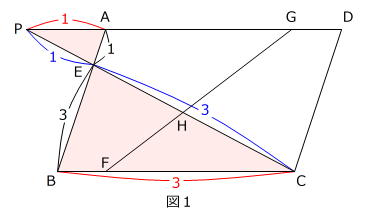
よって、ア＝１、イ＝３です。

さらに、ＰＥ＝①、ＣＥ＝③ とすると、

ＥＨ：ＨＣ：ＥＣ＝４：５：（４＋５）＝４：５：９

ですから、

③＝９　→　①＝３

より、

ＰＨ：ＣＨ＝（３＋４）：５＝７：５

です。

ところで、三角形ＧＰＨと三角形ＦＣＨは相似で、

ＰＨ：ＣＨ＝７：５

ですから、

ＧＰ：ＦＣ も ７：５ です。（図２）

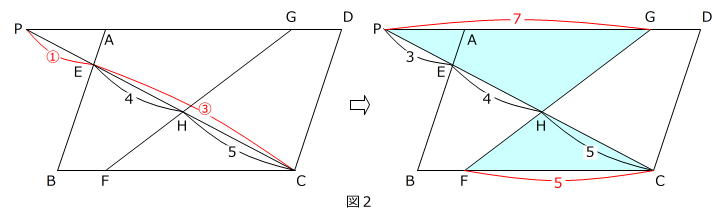
よって、ウ＝７、エ＝５です。

次に

ＢＦ：ＦＣ：ＢＣ＝１：４：（１＋４）＝１：４：５、

ＡＰ：ＢＣ＝１：３

より、ＢＣ＝１５□ とすると、

ＦＣ＝１５□×４/５＝１２□

ＡＰ＝５□

です。

また、

ＧＰ：ＦＣ＝７：５

ですから、

ＧＰ＝１２□×７/５＝１６.８□

です。（図３）

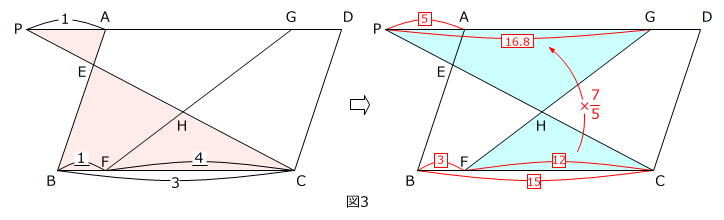
よって、

ＡＧ：ＧＤ＝（１６.８－５）：｛１５－（１６.８－５）｝＝１１.８：３.２＝５９：１６

です。　→　オ＝５９、カ＝１６

答え　ア　１、　イ　３、　ウ　７、　エ　５、　オ　５９、　カ　１６

（２）

（２）では、（１）でわかったこと、高さの等しい三角形は底辺の比と面積比が等しいことの２つを利用していきます。

（１）より、高さの等しい三角形ＧＣＡと三角形ＧＣＤは底辺の比が

ＡＧ：ＧＤ＝５９：１６

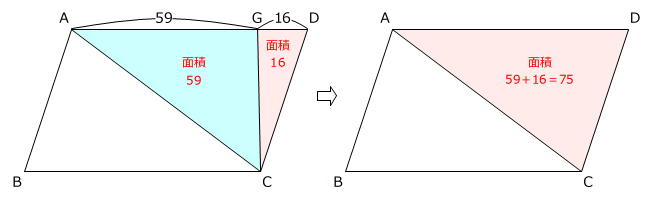
ですから、面積比も ５９：１６ です。（左下図）

よって、三角形ＡＣＤの面積が

５９＋１６＝７５

なので（右下図）、三角形ＧＣＤの面積は三角形ＡＣＤの面積の

１６÷７５＝１６/７５倍

です。

また、

ＰＡ：ＰＧ：ＡＧ＝５：１６.８：（１６.８－５）＝２５：８４：５９

ですから、三角形ＧＣＤの面積を１６とすると三角形ＧＣＰの面積は８４です。（左下図）

（１）より

ＰＨ：ＨＣ＝（３＋４）：５＝７：５

ですから、三角形ＧＨＰの面積を⑦とすると三角形ＧＨＣは⑤です。（右下図）

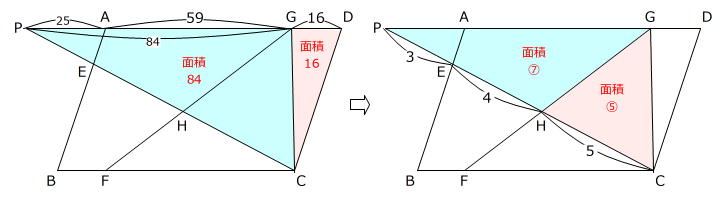
⑦＋⑤＝８４　→　①＝７

７×５＝３５　…　三角形ＧＣＨの面積

７５×２＝１５０　…　平行四辺形ＡＢＣＤの面積

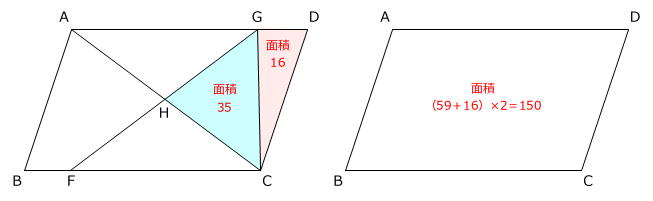
よって、四角形ＧＨＣＤの面積は平行四辺形ＡＢＣＤの面積の

（３５＋１６）÷１５０＝１７/５０倍

です。

答え　キ　１６/７５、　ク　１７/５０

本問は、直線ＰＣを共有する２組の相似な三角形を利用する問題です。

２組の相似を作るための補助線が加えられた図や問題文自体がヒントとなっていますので、誘導に沿って解いていきましょう。

２問目は「相似な三角形を作る（相似完成）」問題です。

【問題】下の図のように、正方形ＡＢＣＤがあります。辺ＡＢを２等分、辺ＢＣを３等分する点をとりました。このとき、次の問いに答えなさい。

① ＥＦの長さはＢＦの長さの何倍ですか。

② 影をつけた部分の面積は何㎠ですか。

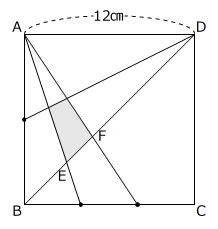
（淑徳与野中学校　第１回　２０２５年　問題２－（３）　問題文一部変更）

【考え方】

①

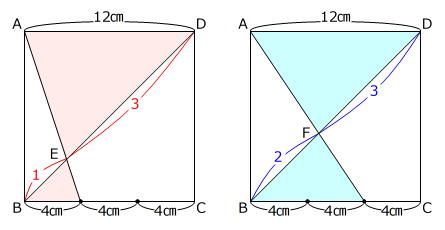
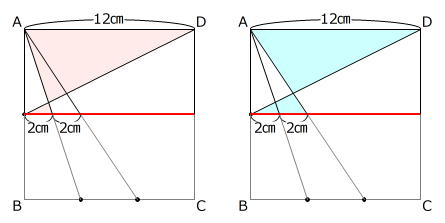
直線ＢＤを共有する２組の相似な三角形に着目します。

左下図の赤色の三角形は相似で、相似比が

４㎝：１２㎝＝１：３

ですから、ＢＥ：ＥＤ も １：３ です。

また、右下図の水色の三角形も相似で、相似比が

８㎝：１２㎝＝２：３

ですから、ＢＦ：ＦＤ も ２：３ です。

次に、ＢＤを分ける比について、連比を使って整理します。

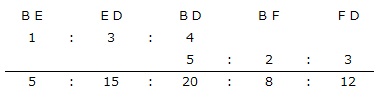
ＥＦ＝ＢＦ－ＢＥ＝８－５＝３

ですから、ＥＦの長さはＢＦの長さの

３÷８＝３/８倍

です。

答え　３/８倍

②

高さの等しい三角形の面積が底辺の比と等しいことを使用します。

三角形ＡＢＤと三角形ＡＥＦは底辺の比が

ＢＤ：ＥＦ＝２０：３

ですから、面積比も ２０：３ です。

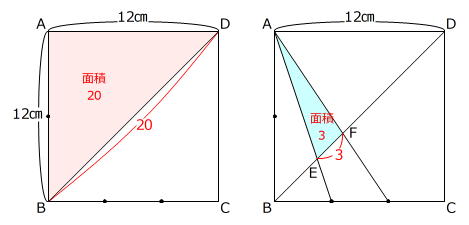
１２㎝×１２㎝×１/２＝７２㎠　…　三角形ＡＢＤの面積

７２㎠×３/２０＝１０.８㎠　…三角形ＡＥＦの面積

さらに、１問目と同じように辺を延長して三角形を作ると、赤線の直角三角形は合同なので、ＨＢ＝１２㎝ です。

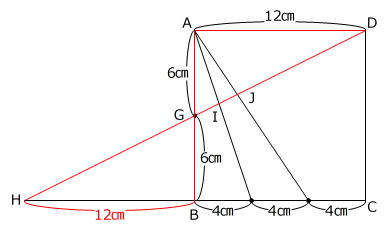
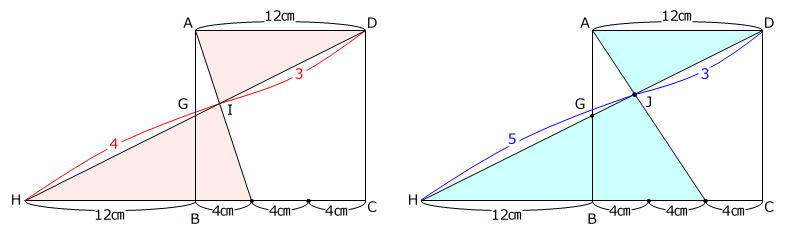
左下図の赤色の三角形は相似で、相似比が

（１２㎝＋４㎝）：１２㎝＝４：３

ですから、ＨＩ：ＩＤ も ４：３ です。

また、右下図の水色の三角形も相似で、相似比が

（１２㎝＋８㎝）：１２㎝＝５：３

ですから、ＨＪ：ＪＤ も ５：３ です。

ＨＤを分ける比について、連比を使って整理します。

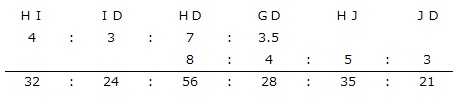
ＩＪ＝ＨＪ－ＨＩ＝３５－３２＝３

三角形ＡＧＤと三角形ＡＩＪは底辺の比が

ＧＤ：ＩＪ＝２８：３

ですから、面積比も ２８：３ です。

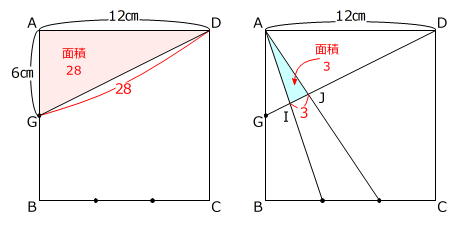
６㎝×１２㎝×１/２＝３６㎠　…　三角形ＡＧＤの面積

３６㎠×３/２８＝２７/７㎠＝３ ６/７㎠　…　三角形ＡＩＪの面積

よって、影をつけた部分の面積は三角形ＡＥＦと三角形ＡＩＪの面積の差の

１０.８㎠－３ ６/７㎠＝６ ３３/３５㎠

です。

答え　６ ３３/３５㎠（２４３/３５㎠）

本問は、直線を共有する相似な三角形の作り方を確認できる問題です。

解答例では、１問目と同じように延長線を利用して図形の「外側」に三角形をつくりましたが、次のように「内側」に作る方法もあります。

今回は、２０２５年度に女子中で出された「相似」の問題をご紹介しました。

これらの「ダブル相似」、「相似完成」とも言われる問題は、とても重要です。

このタイプの問題が苦手なときは、１問目のように相似の作り方や求める順序が誘導になっている問題を練習し、それが解けるようになったら、２問目のように自分で相似を作る問題にチャレンジしましょう。