「第７４４回　女子中の入試問題　平面図形 ２」

前回から、近年の女子中の入試で出された「平面図形」について考えています。

今回は、「平面図形の面積」の問題を見ていきます。

１問目は定番の問題です。

【問題】図のように、１辺の長さが１２㎝の正三角形と３つの半円が重なっています。影をつけた部分の面積は何㎠ですか。円周率を使う場合は３.１４としてください。

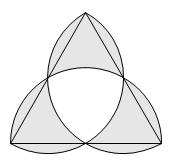
（フェリス女学院中学校　２０２５年　問題１－（２）　問題文一部変更）

【考え方】

弓形は

・おうぎ形－三角形

・移動する

が考え方の基本です。

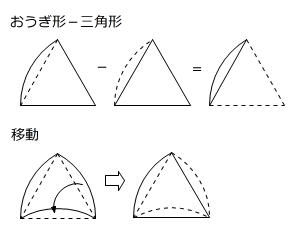
ここでは「移動」を利用することにします。

１２㎝÷２＝６㎝

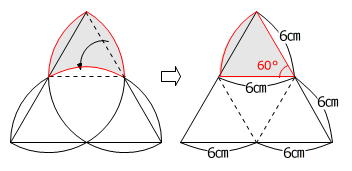
図のように、弓形を移動させると影をつけた部分は半径６㎝、中心角６０度のおうぎ形になります。

６㎝×６㎝×３.１４×６０度/３６０度×３＝５６.５２㎠

答え　５６.５２㎠

本問は、弓形の考え方を確認できる定番の問題です。

特別な条件がない限り正三角形の面積を求めることはできませんので、「おうぎ形－三角形」ではなく、「移動」という方針が選べることを確認しましょう。

２問目も、定番の問題です。

【問題】下の図は、１辺の長さが４㎝の正方形と、半円、おうぎ形を組み合わせたものです。影をつけた部分①の面積と、影をつけた部分②の面積の差を答えなさい。ただし、円周率は３.１４とします。

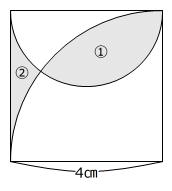
（浦和明の星女子中学校　第一回　２０２５年　問題１－（４）　問題文一部変更）

【考え方】

面積を求める公式のない２つの図形の差を求めるときは、２つの図形に共通な図形をつけ足して面積公式の利用できる図形にすることが、基本の考え方です。

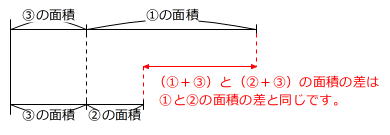
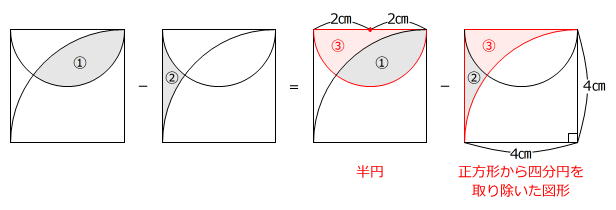
２㎝×２㎝×３.１４÷２＝６.２８㎠　…　（①＋③）の面積

４㎝×４㎝－４㎝×４㎝×３.１４÷４＝３.４４㎠　…　（②＋③）の面積

６.２８㎠－３.４４㎠＝２.８４㎠

答え　２.８４㎠

本問は、面積を求める公式のない図形の面積の差を求めるときの考え方を確認できる問題です。

「『差（または等しい）』とくれば、つけ足し」のようにして覚えておくと便利です。

３問目は、定番問題の図形を別の図形に置き換えた問題です。

【問題】下の図のように、正八角形と直角二等辺三角形が重なっています。正八角形の面積は１００㎠です。また、点Ｏは正八角形の対称の中心です。重なった部分の面積を求めなさい。

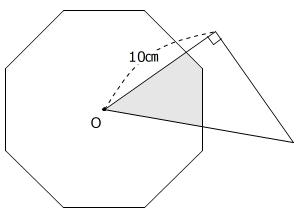
（頌栄女子学院中学校　第１回　２０２５年　問題１－（９）　問題文一部変更）

【考え方】

定番問題の「２つの正方形の重なり」（下図）を、「正八角形と直角二等辺三角形の重なり」に置き換えた問題です。

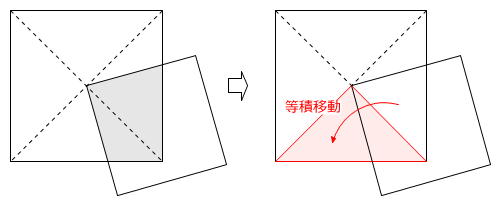
角の大きさに着目します。

正八角形に着目すると

３６０度÷８＝４５度＝○＋□

直角二等辺三角形に着目すると

●＋□＝４５度

ですから、○＝● です。

よって、正八角形と直角二等辺三角形が重なった部分の一部を等積移動させることができます。

移動させると、正八角形を８等分してできる二等辺三角形１つ分になります。

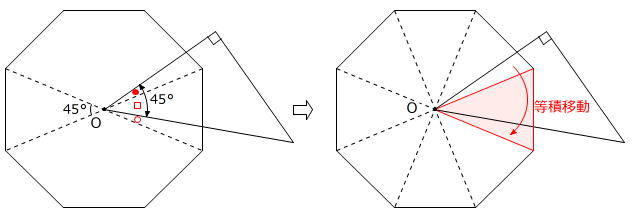
１００㎠÷８＝１２.５㎠

答え　１２.５㎠

本問は、合同と等積移動を利用する問題です。

定番問題と同じように考えることができることを確認しましょう。

４問目からは、応用レベルの問題を見ていきます。

【問題】直径１２㎝の円の周上に円周を１２等分する点をとります。色のついた部分の面積の和は何㎠ですか。円周率は３.１４として計算してください。

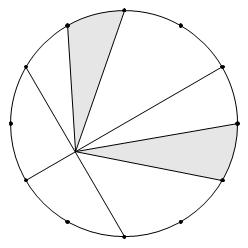
（洗足学園中学校　第１回　２０２５年　問題２－（４）　問題文一部変更）

【考え方】

問題図を時計回りに３０度回転させると、直径が水平になるので見やすくなります。

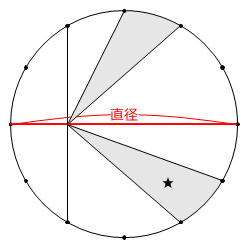
円は直径を対称の軸とした線対称な図形ですから、★の部分を上側に等積移動することができます。

移動させると、色のついた部分は円周の一部（弧）を含むを１つの図形になります。

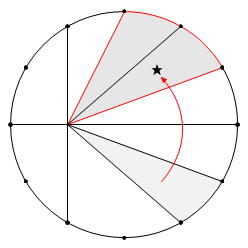
この図形は面積を求める公式のない図形なので、「分ける」、「まわりから引く」という２つの方針が立ちます。

さらに、「弧を含む図形は、弧の両端と円の中心を結んでおうぎ形を作る」を利用すると、求める図形の面積は

（直角三角形）＋（おうぎ形）－（三角形）

で求められることがわかります。

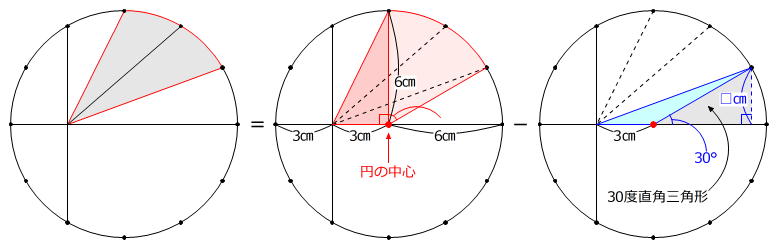
３㎝×６㎝÷２＋６㎝×６㎝×３.１４×６０度/３６０度＝２７.８４㎠　…　赤色部分の面積の和

正三角形を半分にした「３０度直角三角形（右上図の影をつけた部分）」は、「（一番長い辺）÷２＝（一番短い辺）」ですから、

□㎝＝６㎝÷２＝３㎝

です。

３㎝×３㎝÷２＝４.５㎠　…　水色部分の面積

２７.８４㎠－４.５㎠＝２３.３４㎠

答え　２３.３４㎠

本問は、おうぎ形の弧を含む図形の考え方を確認できる問題です。

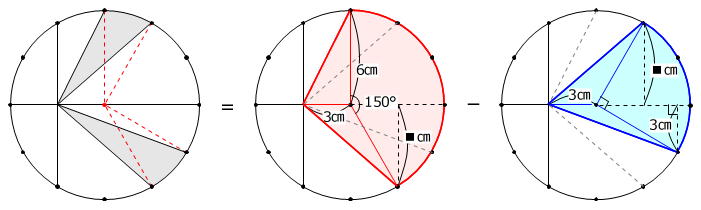
なお、次のように、色のついた部分を一部移動させずにそのままの状態で解くこともできます。

最後の問題です。

【問題】

下図のように、正三角形の中に、正方形と円があります。影の部分の面積を求めなさい。ただし、円周率は３.１４とします。

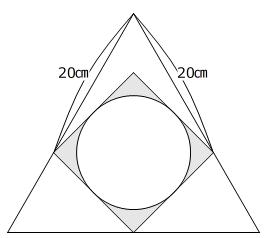
（東洋英和女学院中学部　Ｂ　２０２５年　問題５）

【考え方】

正方形の対角線の真ん中の点と円の中心が重なっていますから、正三角形ＡＢＣと正方形の半分である直角二等辺三角形ＢＣＤと半円Ｏは、図１のように重なります。

また、図２のように、円Ｏの半径を□㎝とすると、正方形ＢＥＣＤの１辺の長さは（□×２）㎝、対角線の長さは２０㎝ですから、

（□×２）㎝×（□×２）㎝＝２０×２０÷２

□×□＝２００÷４＝５０（㎠）

です。

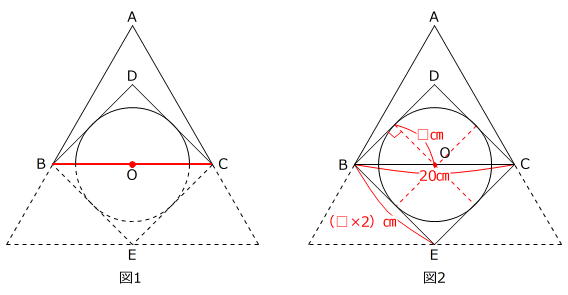
よって、影の部分の面積は

２０㎝×２０㎝÷２－□㎝×□㎝×３.１４＝２００㎠－５０㎠×３.１４＝４３㎠

です。

答え　４３㎠

本問は、半径の長さを求めることができないときの円の面積の求め方を確認できる問題です。

正方形の対角線の真ん中の点と円の中心が重なっていることから、正三角形と直角二等辺三角形の辺と半円の直径が重なることに気づければ、そこから先の考え方は定番です。

解き方の糸口を見つけられないようでしたら、ヒントとして正三角形と直角二等辺三角形の辺と半円の直径が重なることを与えてみましょう。

今回は、２０２５年度に女子中で出された「平面図形の面積」の問題をご紹介しました。

弓形、共通部分のつけ足し、等積移動、弧を含む図形、半径のわからない円など、いずれも大切な解法知識です。

特に１～３問目の基本に「抜け」があれば、できるだけすぐに覚え直すようにしましょう。