「第７４３回　女子中の入試問題　平面図形 １」

前回まで、近年の女子中の入試で出された「速さ」の問題を取り扱いました。

今回からは「平面図形」の問題を見ていきます。

その１回目のテーマは、「角の大きさ」です。

さっそく問題を見ていきましょう。

１問目は、正□角形（正多角形）に関する基本レベルの問題です。

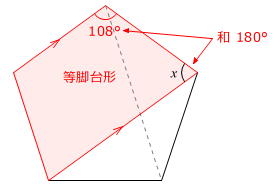
【問題】図のように、正五角形の対角線を２本引きました。角xの大きさは何度ですか。

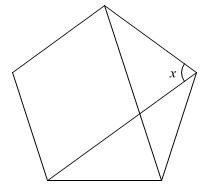
（山脇学園中学校　Ｃ　２０２５年　問題１－（７）　問題文一部変更）

【考え方】

角の大きさを求めるときは、原則として、三角形の角に着目します。

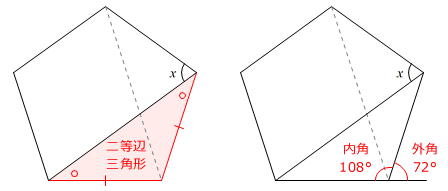
問題図の中に、二等辺三角形があります。（左上図）

また、□角形（多角形）の外角の和は３６０度なので、正五角形の１つの外角の大きさは

３６０度÷５＝７２度

正五角形の１つの内角の大きさは

１８０度－７２度＝１０８度

です。（右上図）

よって、二等辺三角形の印（○）をつけた角の大きさは

（１８０度－１０８度）÷２＝３６度

です。

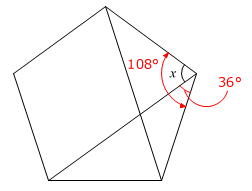
x＝１０８度－３６度＝７２度

答え　７２度

本問は、角の着目ポイントと正多角形の角の基本を確認できる問題です。

□角形の内角の和＝１８０度×（□－２）

と

□角形の外角の和＝３６０度

は、セットで覚えるようにします。

なお、解答例では「１８０度－外角＝内角」を利用しましたが、「三角形の外角のきまり（三角形の外角＝隣りにない２つの内角の和）」を使って解くこともできます。

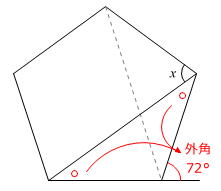
また、正五角形の中にある等脚台形に着目してもＯＫです。

２問目も、二等辺三角形が関係する基本問題です。

【問題】下の図の角アの大きさは何度ですか。ただし、三角形ＡＢＣは正三角形です。

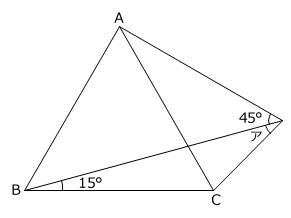
（淑徳与野中学校　第１回　２０２５年　問題２－（１）　問題文一部変更）

【考え方】

角の問題の原則は、１問目で見たように「三角形に着目」ですが、角アに関係のある三角形（三角形ＡＣＤ、三角形ＢＣＤ、三角形ＣＤＥ）について、わかることがまだありません。

次に「三角形ＡＢＣは正三角形」という条件に着目すると、角ＡＢＤの大きさが

６０度－１５度＝４５度

なので、三角形ＡＢＤが直角二等辺三角形であるとわかります。

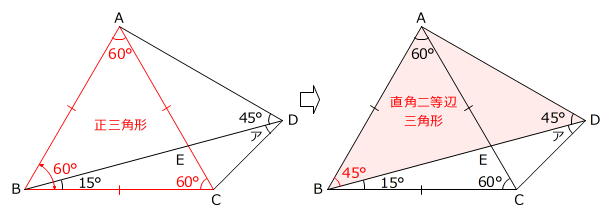
さらに、

角ＣＡＤ＝角ＢＡＤ－角ＢＡＣ＝９０度－６０度＝３０度

ＡＣ＝ＡＤ（＝ＡＢ）

ですから、三角形ＡＣＤが二等辺三角形であることもわかります。

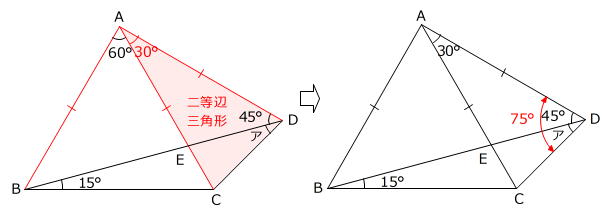
角ＡＤＣ＝（１８０度－３０度）÷２＝７５度

角ア＝角ＡＤＣ－角ＡＤＢ＝７５度－４５度＝３０度

答え　３０度

本問は、「隠れた」二等辺三角形を利用する問題です。

角の大きさを求める問題には、１問目で利用した三角形の内角や外角に着目する問題のほか、本問のように二等辺三角形を見つけて解く問題もあります。

３問目は、平行線と角の基本問題です。

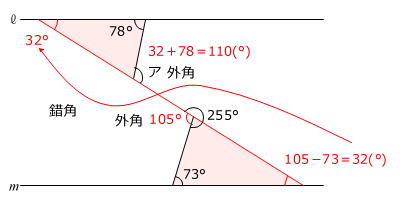
【問題】図の直線ℓとmは平行です。アの角の大きさは何度ですか。

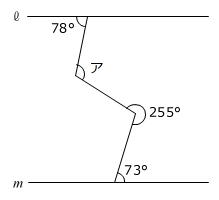
（普連土学園中学校　１日午後算数　２０２５年　問題１－（８））

【考え方】

３問目は、外見から「イナズマ角」とも言われる問題です。

「イナズマ角」は「平行線の同位角や錯角は等しい」を利用して解くことができます。

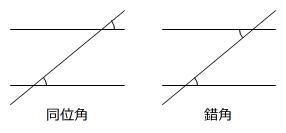
錯角を利用するため、次の図のように直線ℓ、ｍと平行な直線ａ、ｂを引きます。

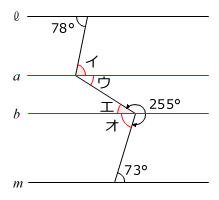
７８度の角とイ、ウとエ、オと７３度の角は、それぞれ錯角の関係ですから、イ＝７８度、ウ＝エ、オ＝７３度です。

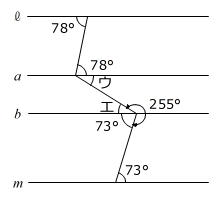
エ＝３６０度－（２５５度＋７３度）＝３２度＝ウ

ア＝イ＋ウ

なので

ア＝７８度＋３２度＝１１０度

です。

答え　１１０度

本問は、平行線の同位角や錯角の利用を確認できる問題です。

解答例の他、次のように「三角形の外角のきまり」を使う解き方もあります。

最後は、補助線を使った応用レベルの問題です。

【問題】下の図は、同じ大きさの２つの正方形を組み合わせたものです。点Ｇは直線ＣＥ上にあります。このとき、角ＡＨＣの大きさは何度ですか。

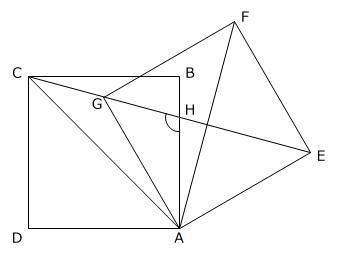
（香蘭女子学院中等科　第１回　２０２５年　問題１－⑪　問題文一部変更）

【考え方】

同じ大きさの正方形を問題図のように組み合わせてできる図形は線対称で、線対称の軸はＡＩです。

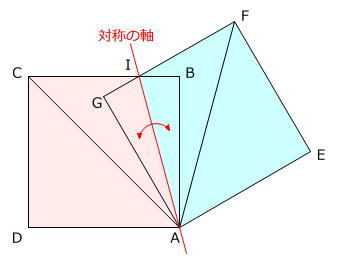
三角形ＡＣＪと、線対称な位置にある２点Ｃ、Ｆを直線で結んでできる三角形ＦＣＪは、ＡＦとＥＧが正方形ＡＥＦＧの対角線なので垂直に交わり、角ＡＪＣ＝角ＦＪＣ＝９０度 ですから、合同な直角三角形です。

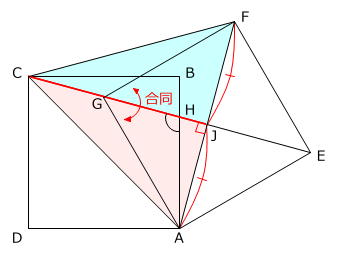
ですから、ＡＣ＝ＦＣ です。

また、ＡＣとＡＦは大きさが同じ正方形の対角線ですから ＡＣ＝ＡＦ です。

よって、三角形ＡＣＦは正三角形とわかります。

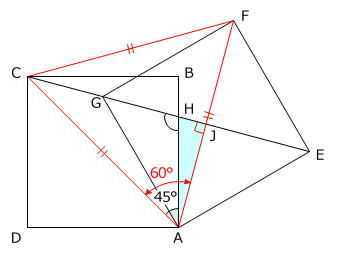
上の図の水色の三角形ＡＨＪにおいて、

角ＡＪＨ＝９０度

角ＨＡＪ＝角ＣＡＦ－角ＣＡＨ＝６０度－４５度＝１５度

ですから、

外角ＡＨＣ＝角ＡＪＨ＋角ＨＡＪ＝９０度＋１５度＝１０５度

です。

答え　１０５度

本問は、１つの頂点で重なる２つの同じ大きさの正方形の特徴と合同な三角形を利用する応用レベルの問題です。

今回は、２０２５年度に女子中で出された「角の大きさ」の問題をご紹介しました。

１～３問目は、三角形の内角や外角、二等辺三角形の角、平行線の角などを利用する基本問題です。もし、正解できない問題があれば、角の問題の原則や着目ポイントをチェックします。

４問目は、対称な図形や三角形の合同なども利用しますので、これらの単元を学習を終えていたら挑戦してみましょう。