第742回 女子中の入試問題 速さ 5
「第742回 女子中の入試問題 速さ 5」
前回は、近年の女子中の入試で出された「速さのグラフ」の問題について考えました。
今回は「通過算」、「流水算」、「時計算」の問題を見ていきます。
1問目は「通過算」の基本問題です。
【問題】長さが200mの列車と300mの列車がそれぞれ一定の速さで動いています。2つの列車が出会ってからすれ違いきるまでに20秒かかり、長さが300mの列車が200mの列車に追いついてから追いこすまでに1分40秒かかりました。長さが200mの列車の速さは秒速何mか求めなさい。
(頌栄女子学院中学校 第1回 2025年 問題1-(5))
【考え方】
通過算は、列車の1点に着目して条件を絵(線分図)に表すと考えやすいです。
このとき、2つの列車がすれちがい終えたときに接している点や追い越し終えたときに接している点に着目すると、列車の動きを表す→について考えやすくなります。
1分40秒=100秒
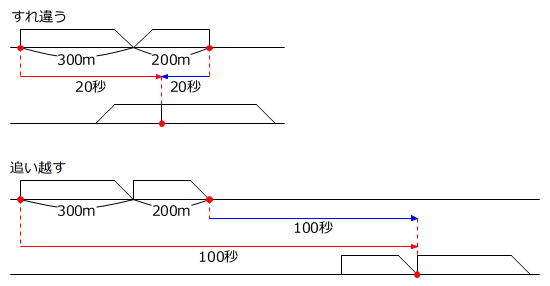
「すれ違う」図からは、2つの列車が20秒間に合わせて
300m+200m=500m
進むことがわかります。
500m÷20秒=25m/秒 … 2つの列車の速さの和
また、「追い越す」図から、長さが300mの列車の方が200mの列車よりも100秒間で
300m+200m=500m
長く進むことがわかります。
500m÷100秒=5m/秒 … 2つの列車の速さの差
和差算を利用すると、長さが200mの列車の速さは
(25m/秒-5m/秒)÷2=10m/秒
と求められます。
答え 秒速10m
本問は、通過算の基本を確認できる問題です。
通過算は、図をかくことで考えやすくなります。
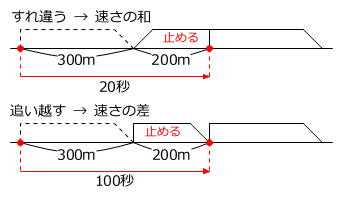
なお、解答例では2つの列車をが動く図をかきましたが、「遅い列車の動きを止める」図で考えることもできます。
2問目は「流水算」の基本問題です。
【問題】ある川沿いの上流にP町、下流にQ町があり、その間を船Aが往復します。船Aは、午前9時30分にP町を出発し、午前11時30分にQ町に着きました。その後午後1時にQ町を出発し、P町に向かいました。船Aの静水での速さを時速16㎞、川の流れの速さを時速4㎞、船Aの静水での速さと川の流れの速さはそれぞれ一定とします。ただし、船の長さは考えないものとします。
(1) P町とQ町は、何㎞はなれていますか。
(2) 午後1時に出発した船AがP町に着くのは、午後何時何分ですか。
(3) 船Bが午後2時にP町を出発して午後4時30分にQ町に着きました。船Aが午後1時にQ町を出発したとき、P町から何㎞はなれたところで船Bとすれちがいますか。ただし、船Bの静水での速さは一定とします。
(白百合学園中学校 2025年 問題2)
【考え方】
(1)
はじめに、船Aの速さ、P町とQ町の間を往復する様子をそれぞれ線分図で表します。
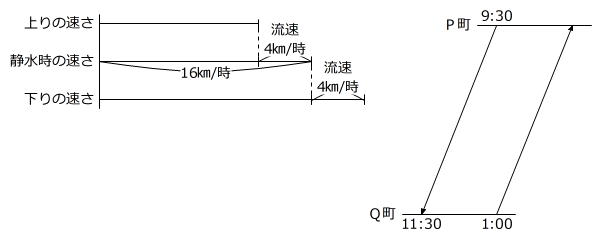
速さの線分図から
16㎞/時-4㎞/時=12㎞/時 … 船Aの上りの速さ
16㎞/時+4㎞/時=20㎞/時 … 船Aの下りの速さ
とわかります。
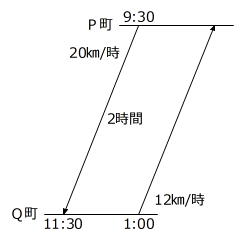
11時30分-9時30分=2時間 … 船AがP町からQ町まで下る時間
20㎞/時×2時間=40㎞
答え 40㎞
(2)
40㎞÷12㎞/時=10/3時間=3時間20分
1時+3時間20分=4時20分
答え 午後4時20分
(3)
2つの船が動く様子を線分図で表します。
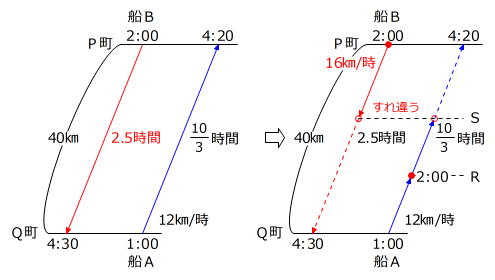
左上の図より船Bが下る速さは
40㎞÷(4時30分-2時)=16㎞/時
とわかります。
また、右上の図で船BがP町を午後2時に出発するとき、船AはQ町から
12㎞/時×(2時-1時)=12㎞
離れたR地点にあります。
船BがP町からすれ違うS地点までにかかる時間と船AがR地点からS地点までにかかる時間は同じ(●~○)ですから、速さの比と距離の比は等しい関係です。
速さの比 (船Bが下る速さ):(船Aが上る速さ)=16㎞/時:12㎞=4:3
↓
距離の比 (PS間):(RS間)=4:3
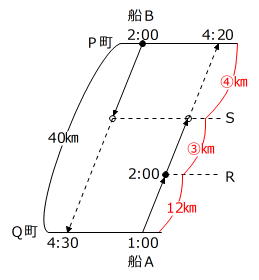
40㎞-12㎞=28㎞ … PR間の距離
④㎞+③㎞=28㎞ → ①㎞=28㎞÷(4+3)=4㎞
④㎞=4㎞×4=16㎞
答え 16㎞
本問は、流水算の基本を確認できる問題です。
流水算は、上りの速さ、下りの速さ、静水時の速さ、流速の関係を表す線分図と船が動く様子を表す線分図をかくと考えやすくなります。
なお、(2)では「速さと比」の利用しましたが、2つの船がすれ違う時刻を求める方法もあります。
2時+(40㎞-12㎞)÷(16㎞/時+12㎞/時)=3時 … すれ違う時刻
16㎞/時×(3時-2時)=16㎞
最後は「時計算」の基本問題です。
【問題】3時から4時までの間に、時計の長針と短針のつくる角度が60°になるのは、3時何分と何分ですか。早い方から順に答えなさい。
(立教女学院中学校 2025年 問題1-(6) 問題文一部変更)
【考え方】
時計算は、はじめに□時00分の図をかくことがポイントです。
このとき、短針を先にかくと、図はかきやすくなります。
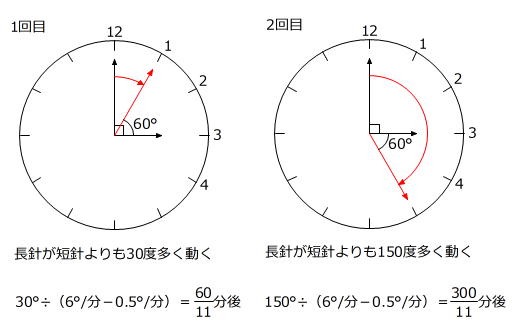
本問では、短針は3時ちょうどに「3」を指していて、その後は「3」と「4」の間にありますから、2つの針がつくる角の大きさがはじめて60度になったときの長針は「1」と「2」の間にあり、2回目のときは「5」と「6」の間にあることがわかります。
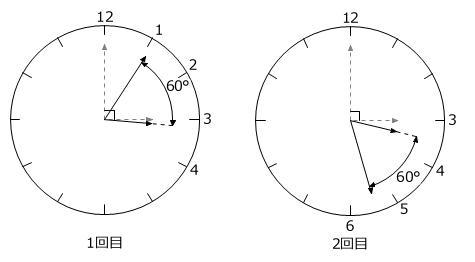
長針と短針が3時ちょうどから動いた角の大きさに着目します。
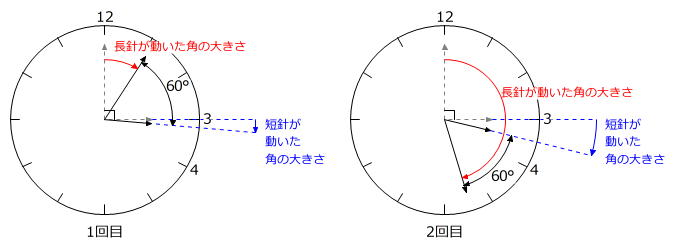
左上図より、2つの針がつくる角の大きさが1回目に60度になったとき
(長針が動いた角の大きさ)+60度=90度+(短針が動いた角の大きさ)
↓
(長針が動いた角の大きさ)-(短針が動いた角の大きさ)=30度
長針が動く速さは分速6度、短針が動く速さは分速0.5度です。
30度÷(6度/分-0.5度/分)=60/11分 → 1回目の時刻は3時5 5/11分です。
右上図より、2つの針がつくる角の大きさが2回目に60度になったとき
(長針が動いた角の大きさ)=90度+(短針が動いた角の大きさ)+60度
↓
(長針が動いた角の大きさ)-(短針が動いた角の大きさ)=150度
150度÷(6度/分-0.5度/分)=300/11分 → 2回目の時刻は3時27 3/11分です。
答え (順に)5 5/11分、27 3/11分
本問は、時計算の基本を確認できる問題です。
時計算は、はじめに□時00分の図をかくと考えやすくなります。
なお、解答例の他に、短針を止めた図をかく解き方もあります。
今回は、2025年度に女子中で出された「通過算」、「流水算」、「時計算」の問題をご紹介しました。
3問とも基本レベルの問題ですので、これらを用いて図のかき方、図の読み取り方、解法知識などの確認をしましょう。
通過算や時計算では、条件をそのまま表す場合と「遅い方の動きを止める」場合の2通りの図のかき方をご紹介していますが、どちらか一方を利用できるようになれば、残りの方にもチャレンジし、どちらの解き方も使えるようになれると理想的です。
![]()




