「第７４８回　女子中の入試問題　平面図形 ６」

前回に引き続き、２０２５年度に女子中の入試で出された「図形の移動」と「点の移動」の問題の中から、今回は前回よりもやや難しい問題を見ていきます。

１問目は、「転がり移動」の問題です。

【問題】１辺の長さが８㎝の正三角形を図のアの位置からイの位置まで、すべらないように転がします。ＡＢ、ＢＣ、ＣＤの長さがすべて８㎝のとき、点Ｐが通ったあとの線の長さは何㎝ですか。

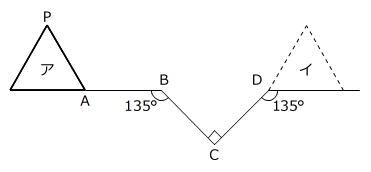
（山脇学園中学校　算数１科　２０２５年　問題１６）

【考え方】

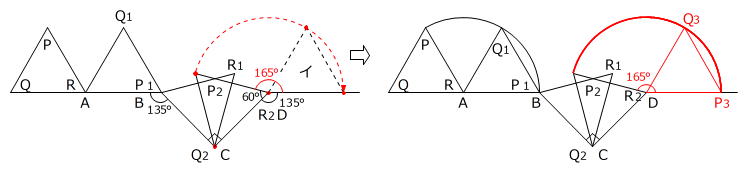
「正三角形の頂点を移動　→　移動した後の頂点を結ぶ」を利用して作図をします。

１. 点Ｒを中心として点Ｐ、点Ｑがそれぞれ １８０度－６０度＝１２０度 回転します。

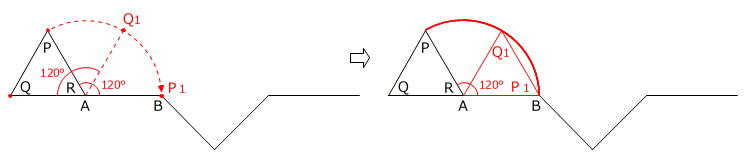
２. 点Ｐ１を中心として点Ｒ、点Ｑ１がそれぞれ ３６０度－（６０度＋１３５度）＝１６５度 回転しますが、点Ｐは移動しません。

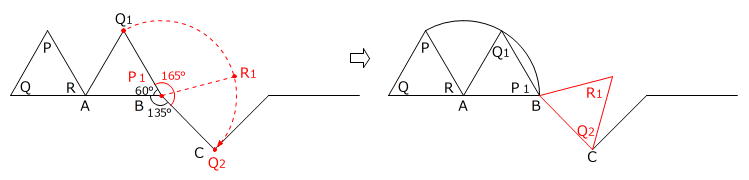
３. 点Ｑ２を中心として点Ｐ１、点Ｒ１がそれぞれ ９０度－６０度＝３０度 回転します。

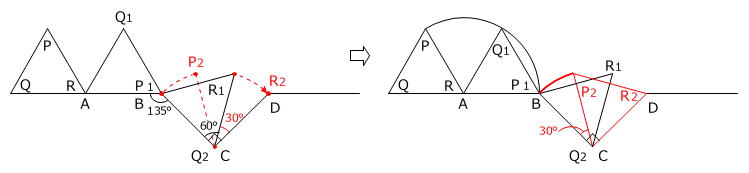
４. 点Ｒ２を中心として点Ｐ２、点Ｑ２がそれぞれ ３６０度－（６０度＋１３５度）＝１６５度 回転します。

８㎝×２×３.１４×（１２０度＋０度＋３０度＋１６５度）/３６０度＝４３.９６㎝

答え　４３.９６㎝

本問は、転がり移動の作図と計算を確認できる問題です。

作図がしづらい場合は、解答例のように一転がりごとの図にしてみましょう。

２問目は、「点の移動」の問題です。

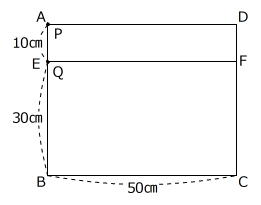
【問題】図のようなＡＢ＝４０㎝、ＢＣ＝５０㎝である長方形ＡＢＣＤがあり、ＥＦはＡＤと平行です。点Ｐは頂点Ａを出発してＢを通ってＣまで、点Ｑは点Ｅを出発してＢ、Ｃを通ってＦまで、それぞれ長方形ＡＢＣＤの辺にそって動きます。ＰとＱは同時に出発し、Ｐは毎秒１㎝、Ｑは毎秒２㎝の速さで動きます。また、ＰはＣに、ＱはＦに着くと、その後はその点にとどまります。このとき、次の問いに答えなさい。

（１） 点Ｐ、Ｑが動き始めてから２０秒後の三角形ＰＱＣの面積を求めなさい。

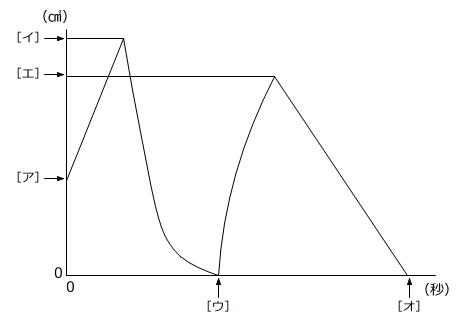
（２） 次のグラフは、点Ｐ、Ｑが動き始めてからの時間と、三角形ＰＱＣの面積の関係を、点ＰがＣに着くまでかいたものです。図の空らん［ア］～［オ］にあてはまる数を求めなさい。

（３）

① 三角形ＰＱＣの面積が３００㎠となるのは全部で何回ありますか。

② 三角形ＰＱＣの面積が２回目に３００㎠となるのは、点Ｐ、Ｑが出発してから何秒後ですか。次の（あ）～（え）から一つ選び、記号で答えなさい。

（あ）１８秒後から２０秒後の間

（い）２１秒後から２３秒後の間

（う）２４秒後から２６秒後の間

（え）２７秒後から２９秒後の間

（田園調布学園中等部　午後入試　２０２５年　問題２　問題文一部変更）

【考え方】

（１）

点Ｐと点Ｑの２０秒後の位置を調べます。

１㎝/秒×２０秒＝２０㎝　…　点Ｐの移動距離

２㎝/秒×２０秒＝４０㎝　…　点Ｑの移動距離

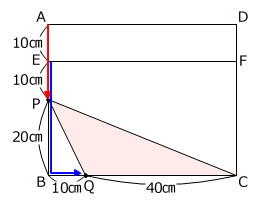
図より、三角形ＰＱＣの面積は

４０㎝×２０㎝÷２＝４００㎠

です。

答え　４００㎠

（２）

グラフは、動く点が図形の頂点を通過するときや動きが止まるときに変化します。

（１０㎝＋３０㎝）÷１㎝/秒＝４０秒後　…　点Ｐが頂点Ｂを通過する

（１０㎝＋３０㎝＋５０㎝）÷１㎝/秒＝９０秒後　…　点Ｐが頂点Ｃに到着する

３０㎝÷２㎝/秒＝１５秒後　…　点Ｑが頂点Ｂを通過する

（３０㎝＋５０㎝）÷２㎝/秒＝４０秒後　…　点Ｑが頂点Ｃを通過する

（３０㎝＋５０㎝＋３０㎝）÷２㎝/秒＝５５秒後　…　点Ｑが頂点Ｆに到着する

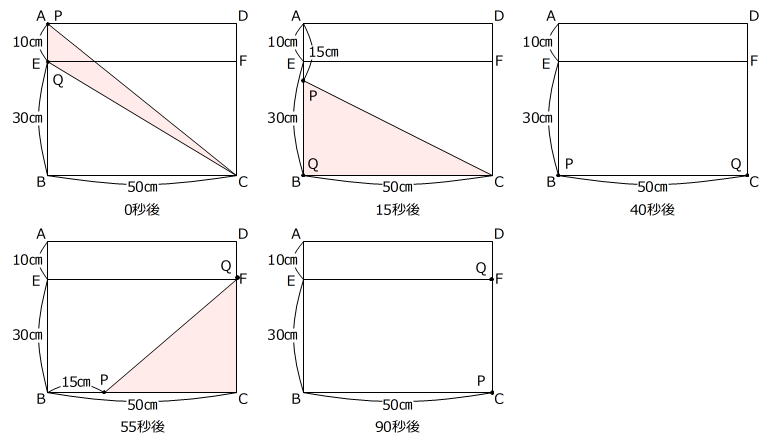
０秒後の三角形ＰＱＣの面積は

１０㎝×５０㎝÷２＝２５０㎠

です。　→　［ア］＝２５０

１５秒後の三角形ＰＱＣの面積は

（４０㎝－１５㎝）×５０㎝÷２＝６２５㎠

です。　→　［イ］＝６２５

４０秒後の三角形ＰＱＣの面積は０㎠です。　→　［ウ］＝４０

５５秒後の三角形ＰＱＣの面積は

（５０㎝－１５㎝）×３０㎝÷２＝５２５㎠

です。　→　［エ］＝５２５

９０秒後の三角形ＰＱＣの面積は０㎠です。　→　［オ］＝９０

答え　ア　２５０、イ　６２５、ウ　４０、エ　５２５、オ　９０

（３-①）

グラフにわかった値を書き込みます。

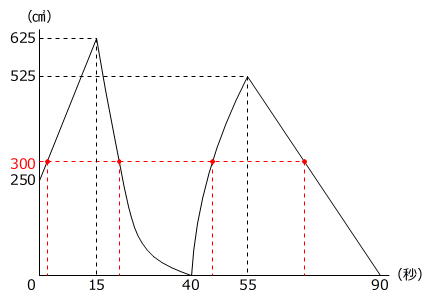
面積が３００㎠の直線をかき加えるとグラフと４か所で交わりますから、三角形ＰＱＣの面積が３００㎠になる回数は４回です。

答え　４回

（３-②）

時間ごとの図をかいて三角形ＰＱＣの面積を調べます。

（あ）

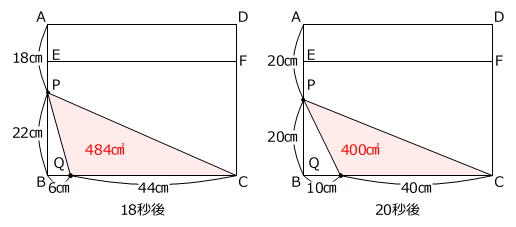
１８秒後の面積は

２２㎝×４４㎝÷２＝４８４㎠

２０秒後の面積は

２０㎝×４０㎝÷２＝４００㎠

なので、１８秒後から２０秒後までに三角形ＰＱＣの面積が３００㎠になることはありません。

（い）

２１秒後の面積は

１９㎝×３６㎝÷２＝３６１㎠

２３秒後の面積は

１７㎝×３４㎝÷２＝２８９㎠

なので、２１秒後から２３秒後までに三角形ＰＱＣの面積が３００㎠になることがあります。

①のグラフより、１５秒後から４０秒後までに三角形ＰＱＣの面積が３００㎠となるのは１回だけです。

答え　（い）

本問は、動く点が図形の頂点を通過するときの図をかく、グラフから読み取るといった考え方を確認できる問題です。

与えられているグラフの中に曲線部分があるため難しそうに見えますが、１問１問は「動く点とグラフ」の基本の考え方で解くことができます。

なお、（３-②）はそれまでの問題を解く過程で面積が平方数になっていること（例：１８秒後　４０－１８＝２２　→２２×２２＝４８４）に気づけると、より早く答えを見つけることができます。

今回は、２０２５年度に女子中で出された「図形の移動」と「点の移動」のやや難しい問題をご紹介しました。

問題の条件が前回よりも少し複雑になっていますが、考え方や用いる解法は基本レベルの問題と同じです。

もし、正解できない問題があるときは、問題の条件の把握にミスがないか、「図形の移動」と「点の移動」の基本の考え方や解法が正しいかなどをチェックしましょう。