「第７４９回　女子中の入試問題　立体図形 １」

前回まで、２０２５年度に女子中の入試で出された「平面図形」について考えました。

今回からは「立体図形」の問題を見ていきます。

その１回目は「立体図形の体積と表面積」の問題です。

１問目は「柱体の表面積」に関する問題です。

【問題】図の立体は円柱を底面に垂直な平面で切りとった立体です。底面の半径が４㎝、中心角が４５度のおうぎ形で、高さが５㎝です。この立体の表面積は何㎠ですか。小数で答えなさい。円周率は３.１４として計算しなさい。

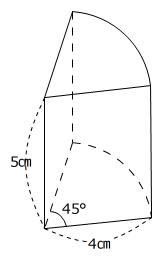
（普連土学園中学校　１日午後算数　２０２５年　問題２８　問題文一部変更）

【考え方】

この立体の展開図は次の通りです。

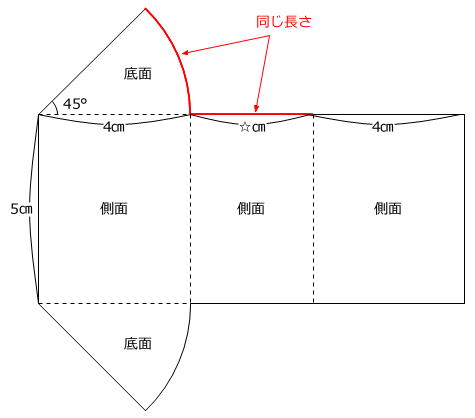
底面であるおうぎ形の弧と接している側面（長方形）の横の長さは同じです（赤線部分）から

☆㎝＝４㎝×２×３.１４×４５度/３６０度＝３.１４㎝

です。

さらに、この立体の３つの側面はどれも縦の長さが立体の高さの５㎝ですから、横の長さが立体の底面の周りの長さと同じ１つの大きな長方形として面積を求めることができます。

５㎝×（４㎝＋３.１４㎝＋４㎝）＝５５.７㎠　…　側面積の和

４㎝×４㎝×３.１４×４５度/３６０度×２＝１２.５６㎠　…　底面積の和

５５.７㎠＋１２.５６㎠＝６８.２６㎠

答え　６８.２６㎠

本問は、柱体の側面積の和を（底面の周りの長さ）×（立体の高さ）を使って求めることができる基本レベルの問題です。

３つの側面積を別々に求めているときは、１つにまとめられることを確認しましょう。

２問目も「柱体の表面積」に関する問題です。

【問題】底面が図のような直角三角形となっている２つの三角柱Ａ、Ｂがあります。Ａの高さはＢの高さよりも３㎝高く、Ａの表面積はＢの表面積よりも３５４㎠大きいです。三角柱Ｂの高さは何㎝ですか。

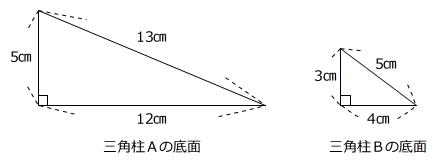
（大妻中学校　第２回　２０２５年　問題８）

【考え方】

三角柱Ｂの高さを□㎝として、２つの三角柱の展開図をかいてみます。

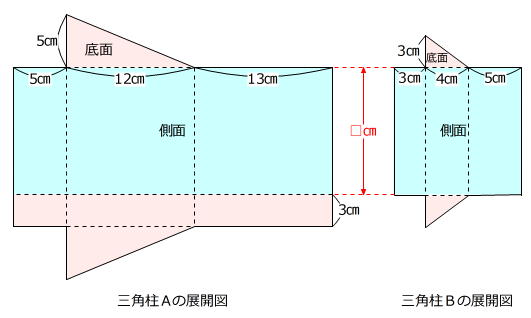
１２㎝×５㎝÷２×２＝６０㎠　…　三角柱Ａの底面積の和

５㎝＋１２㎝＋１３㎝＝３０㎝　…　三角柱Ａの底面の周りの長さ

４㎝×３㎝÷２×２＝１２㎠　…　三角柱Ｂの底面積の和

３㎝＋４㎝＋５㎝＝１２㎝　…　三角柱Ｂの底面の周りの長さ

２つの三角柱の表面積の差が３５４㎠で、図の赤色部分の差が

（６０㎠＋３㎝×３０㎝）－１２㎠＝１３８㎠

ですから、図の水色部分の差は

３５４㎠－１３８㎠＝２１６㎠

とわかります。

□㎝×３０㎝－□㎝×１２㎝＝２１６㎠

□㎝×（３０㎝－１２㎝）＝２１６㎠　

□㎝＝２１６㎠÷１８㎝＝１２㎝　…　三角柱Ｂの高さ

答え　１２㎝

本問は、展開図があると表面積の差という条件を利用しやすい問題です。

見取り図を使って解くこともできますが、もし、正解できないようでしたら展開図をかいてみましょう。

３問目は、「断頭三角柱」と言われる立体の体積を求める問題です。

【問題】次の図の立体は三角柱をある平面でななめに切ったものです。ＡＤが７㎝、ＢＥとＣＦが１２㎝で、三角形ＡＢＣの面積が１５㎠のとき、この立体の体積は何㎤ですか。

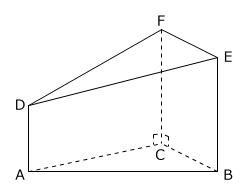
（品川女子学院中等部　算数１教科　２０２５年　問題１７　問題文一部変更）

【考え方】

問題文中の「三角柱をある平面でななめに切った」から、次のように底面積が１５㎠で高さが１２㎝の三角柱から、底面積が１５㎠で高さが５㎝の三角すい（赤色部分）を切りとったと考えることができます。

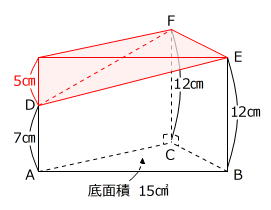
角すいの体積は（底面積）×（高さ）÷３で求めることができます。

１５㎠×１２㎝－１５㎠×５㎝÷３＝１５５㎤

答え　１５５㎤

本問は、三角柱を平面で切ってできる立体の体積の求め方を確認できる問題です。

問題文中のヒントを使って正解を目指しましょう。

なお、（底面積）×（３つの高さの平均）を利用して体積を求めることもできます。

１５㎠×（７㎝＋１２㎝＋１２㎝）/３＝１５５㎤

４問目は、相似を利用する立体図形の問題です。

【問題】下図のような三角柱と円柱の１/４を組み合わせた形の容器があります。この容器に水を入れたところ、水面の高さは底面から６㎝のところになりました。水の体積を求めなさい。ただし、円周率は３.１４とします。

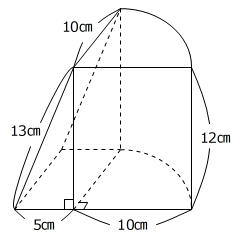
（東洋英和女学院中学部　Ｂ　２０２５年　問題４　問題文一部変更）

【考え方】

水を入れた容器を、三角柱の部分と円柱の１/４の部分に分けます。

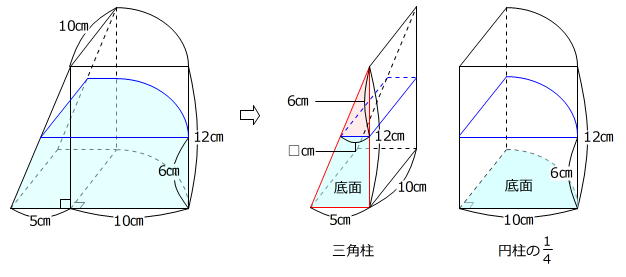
三角柱の底面に着目すると、赤色の三角形の相似比が

１２㎝：（１２㎝－６㎝）＝２：１

なので、

５㎝：□㎝＝２：１　→　□㎝＝２.５㎝

とわかります。

ですから、三角柱の部分の水は、上底が２.５㎝、下底が５㎝、高さが６㎝の台形を底面とする高さが１０㎝の四角柱です。

（２.５㎝＋５㎝）×６㎝÷２×１０㎝＝２２５㎤　…　三角柱の部分の水の体積

また、円柱の１/４の部分の水は、半径が１０㎝、中心角の大きさが９０度のおうぎ形を底面とする高さが６㎝の柱体です。

１０㎝×１０㎝×３.１４×１/４×６㎝＝４７１㎤　…　円柱の１/４の部分の水の体積

２２５㎤＋４７１㎤＝６９６㎤

答え　６９６㎤

本問は、相似を利用して立体図形の辺の長さを求める問題です。

正解できないときは、平面図形の知識である「相似」の使い方が正しいことを確認しましょう。

また、問題文中の「三角柱と円柱の１/４を組み合わせた」をヒントに、水を２つの部分に分けて求めることも大切なポイントです。

今回は、２０２５年度に女子中の入試で出された「立体図形の体積と表面積」の問題をご紹介しました。

角柱や円柱の体積や側面積を求める公式、展開図を利用した表面積の求め方は、立体図形の問題を解く上で大切です。

角すいや円すいの体積や表面積を求める公式は問題文中に書かれていることもありますが、今回の３問目のように与えられていないこともありますから、覚えておくようにします。

また、相似などの平面図形の知識も立体図形の問題でよく使われます。

これらの図形の知識や３問目や４問目のような問題文中のヒントに着目して、立体図形の問題の正答率を高めていきましょう。