第750回 女子中の入試問題 立体図形 2
「第750回 女子中の入試問題 立体図形 2」
前回から、2025年度に女子中の入試で出された「立体図形」の問題を取り扱っています。
今回は「展開図」と「回転体」の問題を見ていきます。
1問目は「展開図の作図」に関する問題です。
【問題】次の図に四角形を1つかき加えると、ある立体の展開図になります。四角形のかき加え方は4通り考えられます。解答用紙の図に、四角形をかき加えて4通りの展開図を完成させなさい。
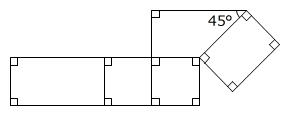
(東京女学館中学校 第2回入試 2025年 問題2-(5))
【考え方】
長方形と台形の図に「四角形を1つかき加える」ので、この立体は四角柱であると予測できます。
さらに、□角柱の側面は長方形や正方形、底面は2つの合同な□角形ですから、問題図に台形を1つかき加えてできる、台形を底面とする四角柱と考えられます。

立体を切り開くと、展開図を作ることができます。
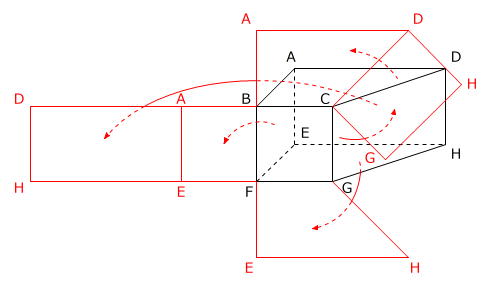
ですから、4通りある展開図のうちの1通りは、四角形BFGCの辺FGとくっつくように台形FEHGをかき加えた図です。
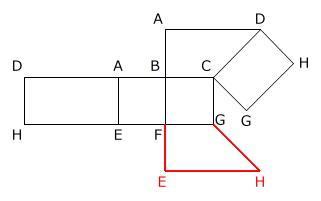
2通り目の展開図は、かき加えた台形FEHGの辺FEと四角形AEFBの辺FEがくっつくように、台形を点Fを中心に時計回りに90度回転させて作ることができます。

さらに、EHが重なるように台形を90度回転させると、3通り目の展開図になります。
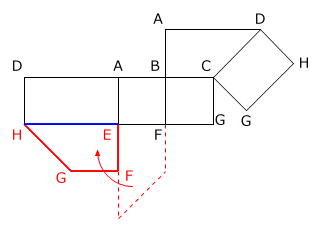
4通り目の展開図は、1通り目の展開図の台形をHGが重なるように回転、移動させて作ることができます。

答え (解説参照)
本問は、展開図のかき方を確認できる問題です。
かいた見取り図の頂点に記号をつけるとそれぞれの面の位置関係がはっきりするので、展開図を作図しやすくなります。
なお、解答例のように「回転させる」と考えずに、見取り図をもとにかき加える台形の位置を考えることもできます。
2問目は「正方形を回転させて作る立体(回転体)の体積」の問題です。
【問題】下の図のような■にぬられた、1辺1㎝の正方形を5個組み合わせた図形があります。直線ℓを軸として1回転させたときにできる立体の体積は何㎤ですか。円周率は3.14とします。
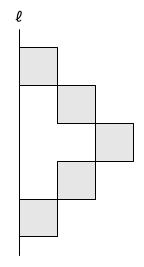
(国府台女子学院中学部 第1回入試 2025年 問題4-(3) 問題文一部変更)
【考え方】
回転体は、回転させる図形を回転の軸と対称な位置にかき、対応する点をなめらかな曲線で結んで見取り図をかくことができます。
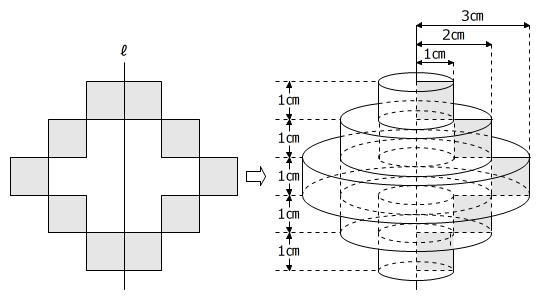
できる立体は高さが1㎝の円柱が2つと、高さが1㎝で穴のあいた円柱3つが集まったもので、次の図のように組み合わせても体積は変わりません。

3㎝×3㎝×3.14×1㎝+2㎝×2㎝×3.14×1㎝=40.82㎤
答え 40.82㎤
本問は、回転体の体積を求める基本レベルの問題です。
正解できないときは、見取り図をかく、体積の求め方を工夫するなどができることを確認しましょう。
3問目は「台形を回転させて作る立体(回転体)の体積」の問題です。
【問題】図の台形を、12㎝の辺のまわりに1回転させてできる立体の体積は何㎤ですか。必要ならば、「(角すい、円すいの体積)=(底面積)×(高さ)÷3」を、また、円周率は3.14を用いなさい。

(山脇学園中学校 C 2025年 問題1-(9) 問題文一部変更)
【考え方】
できる立体の見取り図をかくと、次のようになります。

見取り図から、できる立体は2つの円すいと1つの円柱が集まったものとわかります。
前問と同じように立体を「輪切り」にし、真ん中にある円柱と下側の円すいの位置を入れかえても、体積は変化しません。
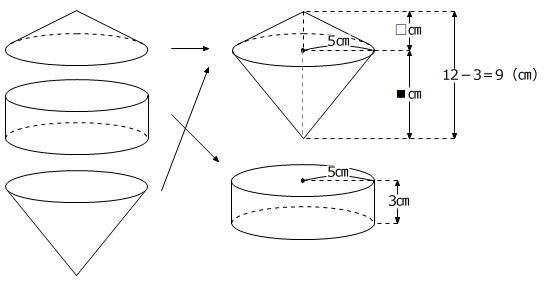
5㎝×5㎝×3.14×□㎝÷3+5㎝×5㎝×3.14×■㎝÷3
=5㎝×5㎝×3.14×(□㎝+■㎝)÷3
=5㎝×5㎝×3.14×(12㎝-3㎝)÷3
=5㎝×5㎝×3.14×9㎝÷3
=75㎤×3.14 … 2つの円すい体積の和
5㎝×5㎝×3.14×3㎝=75㎤×3.14 … 円柱の体積
75㎤×3.14+75㎤×3.14=471㎤
答え 471㎤
本問は、分配のきまりを利用した体積の求め方を確認できる問題です。
なお、円すいの体積が、底面積と高さが同じ円柱の体積の1/3であることから、2つの円すいを1つの円すいに「等積変形(体積)」することもできます。
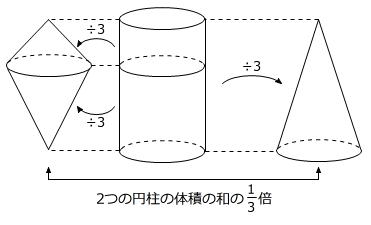
最後は、「回転の軸が回転させる図形の内部を通る」問題です。
【問題】下の図のような平行四辺形を、直線ℓの周りに1回転させてできる立体の体積は何㎤ですか。円周率が必要な場合には3.14として計算しなさい。
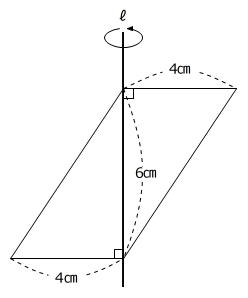
(富士見中学校 第1回 2025年 問題1-(8) 問題文一部変更)
【考え方】
これまでと同じように、回転させる図形を回転の軸と対称な位置もかき、対応する点をなめらかな曲線で結んで、見取り図を作ります。
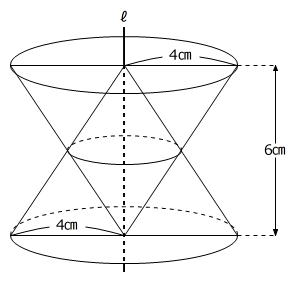
できる立体を輪切りにすると、2つの合同な円すい台に分けられます。
円すい台の体積は、大小の相似な円すいの体積の差として求められます。
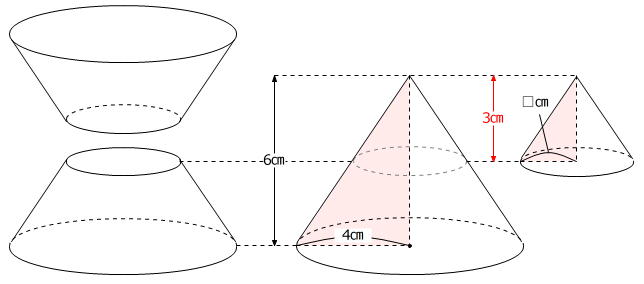
赤色の三角形の相似比が
6㎝:3㎝=2:1
ですから、
4㎝:□㎝=2:1 → □㎝=4㎝×1÷2=2㎝
です。
4㎝×4㎝×3.14×6㎝÷3=32㎤×3.14 … 円すい(大)の体積
2㎝×2㎝×3.14×3㎝÷3=4㎤×3.14 … 円すい(小)の体積
32㎤×3.14-4㎤×3.14=28㎤×3.14=87.92㎤ … 円すい台の体積(1つ分)
87.92㎤×2=175.84㎤
答え 175.84㎤
本問は、円すい台の体積の求め方を確認できる問題です。
もし、正解できないようでしたら、見取り図をかけること、立体を「輪切り」にできること、計算を正確にできることを確認しましょう。
なお、三角形(赤色)の相似比が2:1であることから、体積比が(2×2×2):(1×1×1)=8:1となることを利用して、
2㎝×2㎝×3.14×3㎝÷3×(8-1)=28㎤×3.14=87.92㎤
のように計算することもできます。
今回は、2025年度に女子中の入試で出された「展開図」と「回転体」の問題をご紹介しました。
どの問題も基本の考え方と正確な計算で解く問題です。
間違える問題があれば、作図を含めた考え方と計算のチェック、修正をしましょう。
![]()




