「第７５８回　女子中の入試問題　資料の問題・思考問題」

これまで、２０２５年度に女子中の入試で出された問題について考えてきました。

その最後となる今回は、「資料の整理の問題」と「思考問題」を取り扱います。

１問目は、資料の整理の問題です。

【問題】次の表は、生徒７人が１０問の漢字テストを受けたときの結果を表しています。中央値が７であるとき、Ａさんの正答数として考えられる整数は何通りありますか。

（普連土学園中学校　１日午後算数　２０２５年　問題３３）

【考え方】

Ａさん以外の６人のテスト結果をドットプロットで表してみます。

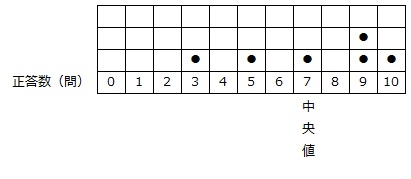
７人÷２＝３.５人

より、Ａさんを含む７人の中央値は、正解数が少ない方（または多い方）から数えて４人目の生徒の正解数です。

しかし、Ａさん以外の６人のテスト結果を表したドットプロット（上の表）を見ると、正解数が７問の生徒は正解数の少ない方から数えて３人目です。

ですから、正解数が７問の生徒が少ない方から数えて４人目となるようなＡさんの正答数となる整数は、０以上７以下の８通りがあります。

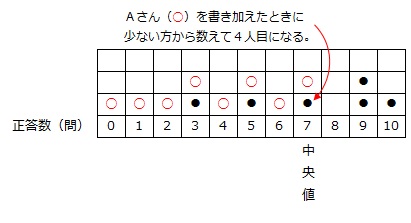
答え　８通り

本問は、資料問題の基本を確認できる問題です。

正解できないようでしたら、中央値の意味や求め方を見直しましょう。

２問目も、資料の整理の問題です。

【問題】２５人の生徒に１０点満点のテストを行い、結果をヒストグラムに表したら下のようになりました。

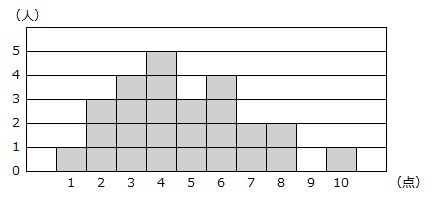
ここで、１人の点数が誤っていることがわかり、修正を行いました。修正の結果、中央値は変わりましたが、最頻値に変化はなく、平均点は修正前後で０.０８点の差がありました、何点から何点に修正されたか求めなさい。

（頌栄女子学院中学校　第１回　２０２５年　問題１－（８））

【考え方】

２５人÷２＝１２.５人

より、２５人の中央値は、点数が低い方（または高い方）から数えて１３人目の生徒の点数です。

下のように、修正前の１点以上４点以下の生徒数が

１人＋３人＋４人＋５人＝１３人

ですから、修正前の中央値は、点数が少ない方から１３人目の生徒の点数の４点です。

また、修正前の最頻値が生徒が５人いる４点ですから、修正後も４点です。

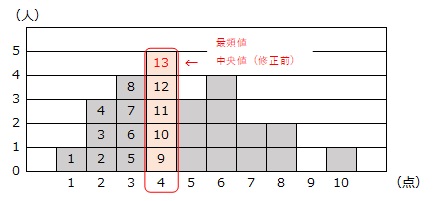
よって、修正後に「１３人目の生徒の点数は４点ではないが、４点の人数が最多」となるのは、下のように、１人目から８人目の生徒のうちの１人が５点以上に移動して、４点以下の合計人数が１２人になる場合です。

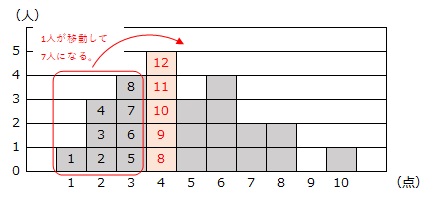
ところで、修正の前後で２５人の平均値に０.０８点の差がありましたから、修正前と修正後の２５人の合計点の差は

０.０８点×２５人＝２点

です。

従って、「移動する１人は、点数が２点高くなって５点以上になる生徒」ということになりますから、３点の生徒が５点に移動したとわかります。

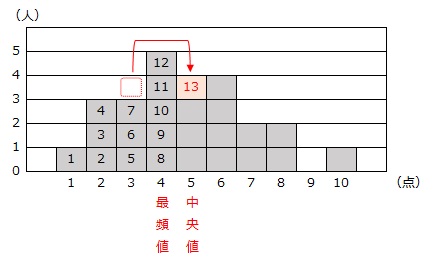
答え　３点から５点に修正された

本問は、資料問題の用語の意味を確認できる問題です。

また、（平均点の差）×（人数）＝（合計点の差）という考え方もポイントになっています。

最後は思考問題です。

【問題】１から１０までの数字が１つずつ書いてある１０枚のカードがあります。英子さんと和子さんがこのカードを５枚ずつ取り、さいころを投げて、出た目の倍数が書いてあるカードの数字の合計を得点とすることにしました。例えば、英子さんが［１］［２］［７］［８］［１０］、和子さんが［３］［４］［５］［６］［９］のカードを取り、さいころの２の目が出た場合、得点は英子さんが２０点、和子さんが１０点になります。さいころを３回投げ、３回の合計得点が高い方を勝ちとします。次の問いに答えなさい。

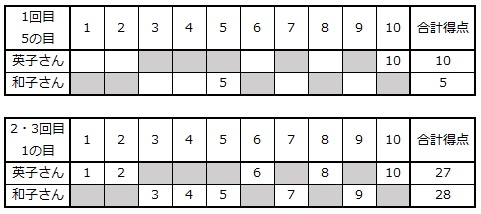
（１） 英子さんが［１］［３］［４］［７］［１０］のカードを取り、さいころの出た目が１、２、４のとき、２人の合計得点はそれぞれ何点ですか。

（２） 英子さんが［６］［８］［１０］を含む５枚のカードを取ったとき、さいころは１回目に５が出て、２回目と３回目に同じ目が出て和子さんが勝ちました。

① ２回目と３回目に出たさいころの目はいくつですか。

② ２人の合計得点はそれぞれ何点ですか。

（東洋英和女学院中学部　Ｂ　２０２５年　問題１１　問題文一部変更）

【考え方】

（１）

さいころを３回投げたときの得点について、表に整理します。

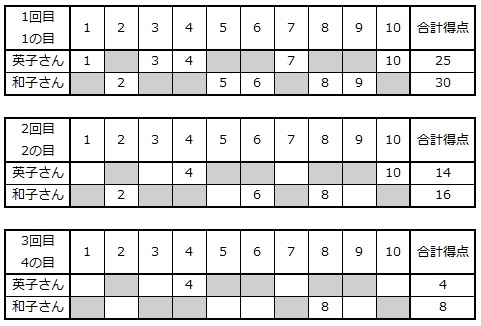
２５点＋１４点＋４点＝４３点　…　英子さん

３０点＋１６点＋８点＝５４点　…　英子さん

答え　英子さん　４３点、　和子さん　５４点

（２）

１回目に５の目が出ましたから、少なくとも英子さんは１０点を得点します。

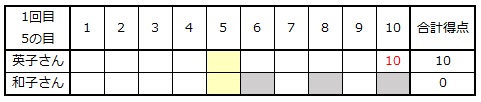
ですから、さいころを３回投げたとき、和子さんが勝つ可能性が高くなると考えられるのは、和子さんが２回目と３回目に［１０］の次に大きな数字である［９］のカードで得点をする場合です。

さいころの目は６以下の整数ですから、［９］のカードで得点できるのは１または３の目が出たときです。

２回目と３回目に１の目が出た場合、英子さんの残り２枚のカードが［１］、［２］、和子さんの残り４枚のカードが［３］［４］［５］［７］であったとしても、英子さんの合計得点が

１０点＋（１点＋２点＋６点＋８点＋１０点）×２＝６４点

和子さんの合計得点が

５点＋（３点＋４点＋５点＋７点＋９点）×２＝６１点

となり、和子さんが勝つことはできません。

２回目と３回目に３の目が出た場合、英子さんの残り２枚のカードが［１］、［２］、和子さんの残り４枚のカードが［３］［４］［５］［７］であれば、英子さんの合計得点が

１０点＋６点×２＝２２点

和子さんの合計得点が

５点＋（３点＋９点）×２＝２９点

となり、和子さんが勝ちます。

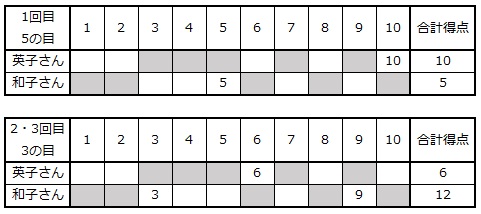
答え　①　３、　②　英子さん２２点、　和子さん　２９点

本問の（１）はルールの確認、（２）はどのような場合に和子さんの勝てる可能性が高くなるかを考える問題です。

「最も数字の大きい［１０］のカードを英子さんに持たれていても和子さんが勝つには…」のように考えるところがポイントになっています。

正解できないようでしたら、解答例のような表を書いて、状況をわかりやすくしてみましょう。

今回は、２０２５年度に女子中で出された「資料の問題・思考問題」をご紹介しました。

資料の整理の問題は用語や整理方法が重要です。

また、思考問題では「もし、○○だったら～」という可能性を考えることや、考えてわかったことを見やすくする整理方法などがポイントになっています。

もし、資料の整理の問題が苦手なようでしたら、中央値や最頻値などの用語の意味やドットプロット、ヒストグラム（柱状グラフ）などの書き方や読み取り方を基本問題で復習しましょう。

思考問題は、受験予定校の過去問などを利用することが一番取り組みやすい方法だと思います。