第757回 女子中の入試問題 文章題 4
「第757回 女子中の入試問題 文章題 4」
ここまで、2025年度に女子中の入試で出された「文章題」の問題を取り扱ってきています。
今回の問題のテーマは「集合算」です。
1問目は、基本レベルの問題です。
【問題】45人のクラスで、兄と姉がいるかどうかを調べました。兄がいる人は33人、姉がいる人は24人、兄も姉もいない人は6人いました。兄と姉が両方いる人は何人ですか。
(共立女子中学校 2/2入試 2025年 問題2-①)
【考え方】
集合算の条件を整理する方法には、相関表、ベン図、線分図があります。
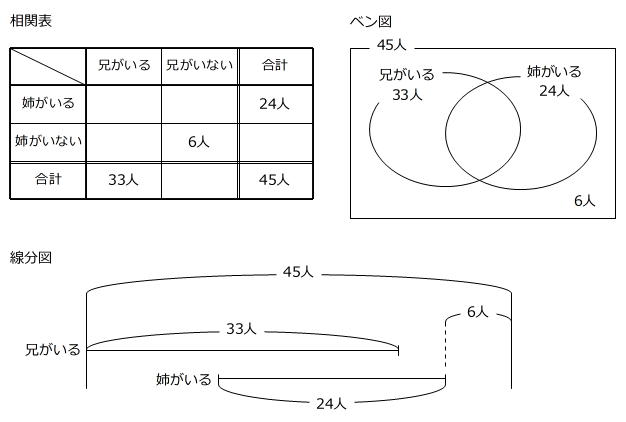
ここでは、ベン図を利用することにします。
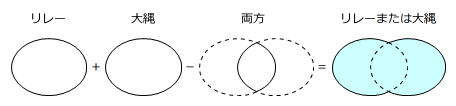
「兄がいる」と「姉がいる」の2つの項目で分類されたベン図には、次のような関係式があります。
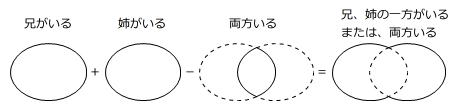
兄と姉の両方がいる人を□人とします。
33人+24人-□人+6人=45人 → □人=63人-45人=18人
答え 18人
本問は、集合算の基本を確認できる問題です。
2つのベン図の関係式が使えることをチェックしましょう。
2問目は「範囲」のある集合算です。
【問題】下の文章の□にあてはまる数を入れなさい。
冬休みに行った場所のアンケートを38人のクラスで取ったところ、遊園地に行った人は22人、動物園に行った人は29人でした。遊園地と動物園の両方に行った人は□人以上□人以下で、両方とも行かなかった人は最大□人です。
(東洋英和女学院中学部 A・帰国生 2025年 問題6)
【考え方】
集合算の条件を整理する3つの方法のうち、ここでは線分図を利用することにします。
範囲のある集合算を線分図で整理するので、「遊園地に行った人」と「動物園に行った人」の線分のうち、どちらか一方だけを動かして考えるようにします。
ここでは、「動物園に行った人」を動かしてみます。
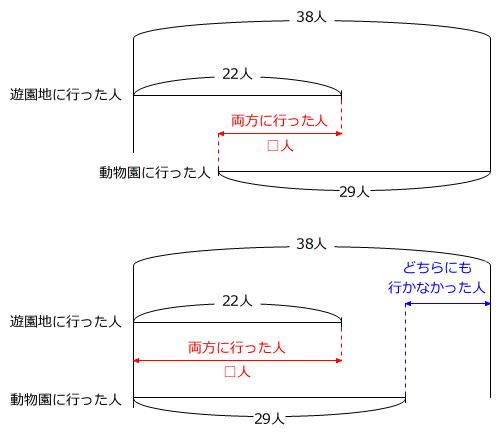
上側の図のように「動物園に行った人」を右側に寄せてかくと、「両方に行った人」が
22人+29人-38人=13人
で最も少なくなり、下側の図のように「動物園に行った人」を左側に寄せてかくと、「両方に行った人」が22人で最も多くなります。
また、両方ともに行かなかった人が最も多くなるのは、下側の図のときで、
38人-29人=9人
です。
答え (順に)13、22、9
本問は、範囲のある集合算の考え方を確認できる問題です。
もし、相関表やベン図を利用して間違えるようでしたら、線分図を使って解き直してみましょう。
3問目は、分類する項目が3つある集合算です。
【問題】ある小学校の6年生50人を対象に10点満点のテストをしました。このテストの問題はA、B、Cの3問で、配点はAが2点、Bが3点、Cが5点です。どの問題も正解か不正解のいずれかです。テストの結果、点数と人数は下の表のようになりました。このテストで正解した問題数が1問のみだった人の平均点は3.1点でした。問題Cを正解した人は、全部で何人ですか。

(鷗友学園女子中学校 第一回 2025年 問題4)
【考え方】
分類する項目が3つある集合算の条件は、ベン図を使って整理することができます。
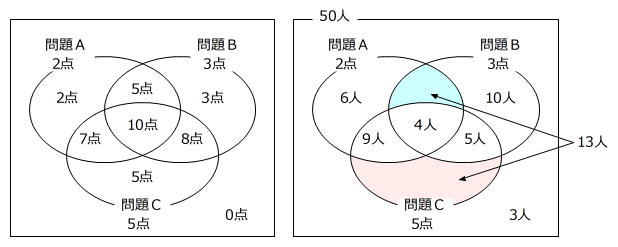
また、「正解した問題数が1問のみだった人」は、2点の人、3点の人、5点の人のうちの赤色部分の人(□人とします)で、これらの人の「平均点は3.1点でした」は次のような面積図に表せます。
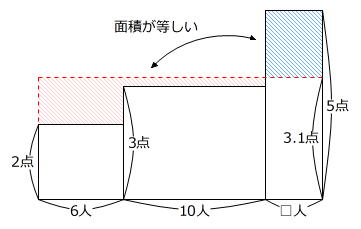
(3.1点-2点)×6人+(3.1点-3点)×10人=7.6点 … 赤色斜線部分の面積=青色斜線部分の面積
□人=7.6点÷(5点-3.1点)=4人 … ベン図の赤色部分
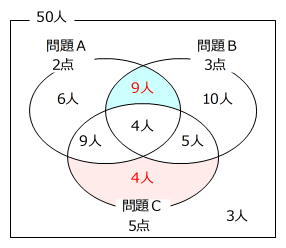
ですから、問題Cを正解した人は
4人+9人+5人+4人=22人
です。
答え 22人
本問は、3つのベン図の基本が確認できる問題です。
最後の問題も、分類する項目が3つある集合算です。
【問題】45人いるクラスの生徒に、体育祭で参加したい種目のアンケートをとりました。種目はリレー、大縄、ドッジボールの3つで、いくつ選んでもよいとしました。アンケートの結果をまとめると以下のようになりました。
・リレーを選んだ人は27人、大縄を選んだ人は17人、ドッジボールを選んだ人は33人。
・大縄とドッジボールの2つのみを選んだ人は9人。
・リレーとドッジボールの2つのみを選んだ人は16人。
・3つとも選んだ人は3人。
・3つとも選ばなかった人はいない。
このとき、リレーのみを選んだ人は何人ですか。
(普連土学園中学校 1日午後算数 2025年 問題50)
【考え方】
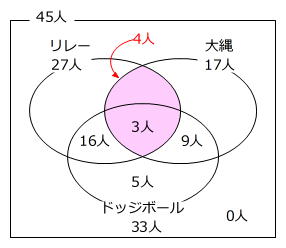
前問と同じように、ベン図に整理してみます。
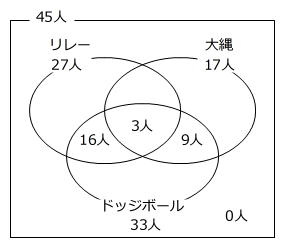
ドッジボールのみを選んだ人(下のベン図の赤色部分)は
33人-(9人+16人+3人)=5人
ですから、リレーまたは大縄を選んだ人(下のベン図の水色部分)は
45人-5人=40人
です。
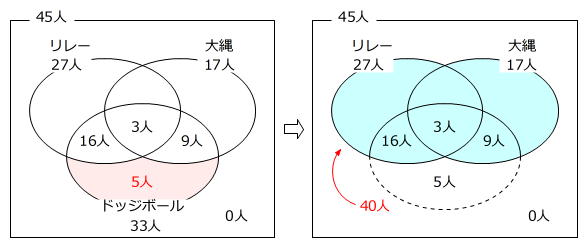
リレーと大縄の両方を選んだ人を□人として、1問目と同じように2つのベン図の関係式を利用します。
27人+17人-□人=40人 → □人=44人-40人=4人(下図の紫色部分)
ですから、リレーのみを選んだ人は
27人-(16人+4人)=7人
です。
答え 7人
本問も、3つのベン図の基本が確認できる問題です。
3つのベン図から1つを取り除いて、2つのベン図にする点がポイントになっています。
今回は、2025年度に女子中の入試で出された「集合算」の問題をご紹介しました。
もし、集合算が苦手なようでしたら、まずは、1問目でみた3つの整理方法のどれか1つのマスターを目指します。
あわせて、2つのベン図の関係式も使えるように練習をしましょう。
それができるようになれば、2問目のように範囲のある問題や、3問目以降の3つの項目で分類する問題にチャレンジしてみるとよいと思います。
![]()




