「第７５６回　女子中の入試問題　文章題 ３」

これまで、２０２５年度に女子中の入試で出された「文章題」について見てきています。

今回は、「差集め算」を中心に取り扱っていきます。

１問目は、差集め算の定番問題です。

【問題】子どもが長いすに座るのに、１脚に４人ずつ座ると３人が座れなくなり、１脚に７人ずつ座ると最後の長いすに５人座り、７脚余ります。長いすの数と子どもの人数をそれぞれ求めなさい。

（東京女学館中学校　第２回　２０２５年　問題２－（１））

【考え方】

「用意した長椅子全部に生徒が座る」場合について考えていきます。

長椅子が□脚あるとします。

７人ずつ座る場合の空席は

（７人－５人）＋（７人×７脚）＝５１人分

です。

差に着目します。

７人×□脚－４人×□脚＝３人＋５１人　→　□脚＝５４人÷（７人－４人）＝１８脚

ですから、子どもの人数は

４人×１８脚＋３人＝７５人（または、７人×１８脚－５１人＝７５人）

です。

答え　長いす　１８脚、　子ども　７５人

本問は、長椅子を題材にした差集め算の考え方を確認できる問題です。

線分図の他に、次のような表に整理して解くこともできます。

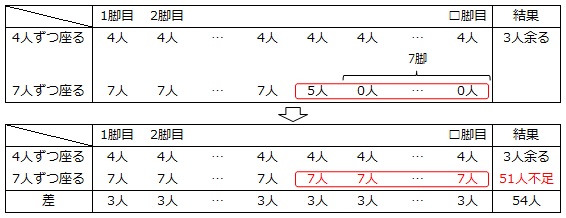
２問目も、差集め算の定番問題です。

【問題】花子さんは９０円のボールペンをちょうど何本か買えるお金を持っています。そのお金で１２０円のシャープペンシルを買うと、買える本数は９０円のボールペンより７本少なくなり３０円残ります。花子さんが持ってるお金はいくらですか。

（洗足学園中学校　第１回　２０２５年　問題２－（２））

【考え方】

ボールペンよりも本数の少ないシャープペンシルの本数を□本とすると、条件を表しやすいです。

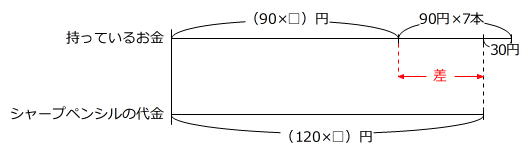
差に着目します。

１２０円×□本－９０円×□本＝９０円×７本－３０円　→　□本＝６００円÷（１２０円－９０円）＝２０本

ですから、花子さんが持ってるお金は

９０円×（２０本＋７本）＝２４３０円（または、１２０円×２０本＋３０円＝２４３０円）

です。

答え　２４３０円

本問も、差集め算の基本を確認できる問題です。

表に整理する場合は、次のように表すことができます。

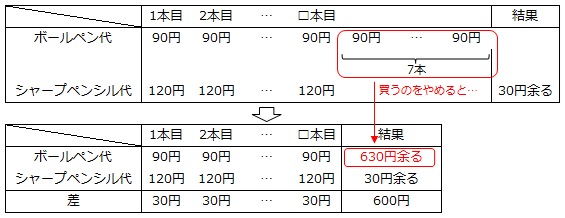
※ 「シャープペンシルをあと７本買うと…」と考える解き方もあります。

３問目は、差集め算以外の考え方も必要になる融合問題です。

【問題】１０円玉、５０円玉、１００円玉があわせて４５枚あり、合計金額は２７３０円です。Ａさんがそれぞれの枚数を数えて合計金額を計算したところ、２種類の硬貨の枚数を入れかえて計算してしまったので、２１００円になりました。１００円玉は何枚ありますか。

（山脇学園中学校　算数１科　２０２５年　問題（９））

【考え方】

枚数を入れかえた硬貨が１０円玉と５０円玉の場合は１枚あたりの差が４０円、１０円玉と１００円玉の場合は１枚あたりの差が９０円、５０円玉と１００円玉の場合は１枚あたりの差が５０円ですから、それぞれの硬貨を何枚かを入れかえると、合計金額の差は４０の倍数、９０の倍数、５０の倍数になります。

２７３０円－２１００円＝６３０円　…　合計金額の実際の差

６３０が９０の倍数ですから、枚数を入れかえた硬貨は１０円玉と１００円玉とわかります。

また、枚数を入れかえると合計金額が減りましたから、実際の枚数は１００円玉の方が１０円玉より多いこともわかります。

６３０円÷９０円＝７枚　→　１００円玉の方が１０円玉よりも７枚多い。

ここからは「３種のつるかめ算」です。

（２７３０円－２６００円）÷１０円＝１３

□＝７＋１３＝２０

答え　２０枚

本問は、取り違えとつるかめ算を含む問題です。

（１枚あたりの差）×（枚数）＝（合計金額の差）という考え方は差集め算の基本ですが、倍数条件の利用が必要になるため、基本問題よりも難しくなっています。

なお、３種のつるかめ算は、次のような面積図で考えることもできます。

最後は、大問形式の問題です。

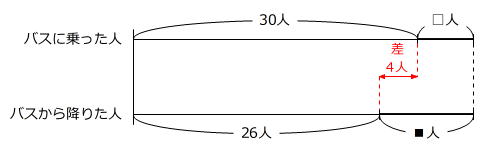
【問題】ある町では、３つの停留所Ａ（始発）、Ｂ、Ｃ（終点）に停まるバスが運行していて、運賃は下の表の通りです。ある１回の運行では、Ａで３０人が乗り、Ｃでは乗っていた２６人全員が降りました。

（１） Ｂから乗った人がいなかったとき、運賃の合計はいくらですか。

（２） Ｂで乗り降りした人の合計が８人だったとき、運賃の合計はいくらですか。

（３） 運賃の合計が１８０００円だったとき、Ｂから乗った人は何人ですか。

（三輪田学園中学校　１回午後　２０２５年　問題４）

【考え方】

（１）

Ｂから乗った人がいないので、Ｃで降りた２６人はＡから乗った人ですから、Ａから乗った残りの

３０人－２６人＝４人

はＢで降りたことになります。

４００円×４人＋６００円×２６人＝１７２００円

答え　１７２００円

（２）

Ｂから乗った人数を□人、Ｂで降りた人数を■人とします。

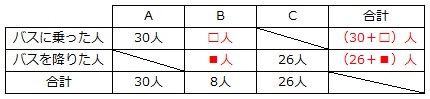
バスに乗った人数の合計とバスから降りた人数の合計は同じですから、□人と■人の差が

３０人－２６人＝４人

とわかります。

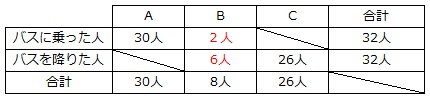
和差算です。

□人＝（８人－４人）÷２＝２人

■人＝８人－２人＝６人

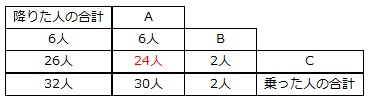
よって、「乗り降り」が「Ａ～Ｂ」の人が２人、「Ｂ～Ｃ」の人が６人、「Ａ～Ｃ」の人が

３０人－６人＝２４人（または、２６人－２人＝２４人）

とわかります。

４００円×６人＋３００円×２人＋６００円×２４人＝１７４００円

答え　１７４００円

（３）

（１）よりＢから乗る人が０人のときの運賃の合計が１７２００円、（２）よりＢから乗る人が２人のときの運賃の合計が１７４００円ですから、Ｂから乗る人が１人増えると運賃の合計が

（１７４００円－１７２００円）÷２人＝１００円

増えることがわかります。

（１８０００円－１７２００円）÷１００円＝８人

答え　８人

本問は、誘導形式の大問です。

（１）、（２）を利用すると（３）が解きやすいことを確認しましょう。

なお、バスの乗降人数を整理するときは、「合計欄」を表に追加すると考えやすくなります。

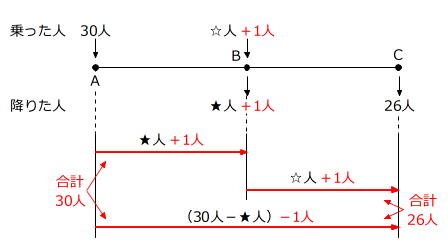
また、（３）では、Ｂから乗る人が１人増えるとＢで降りる人が１人増え、同時にＡからＣまで乗り通す人が１人減るので、運賃の合計は

４００円＋３００円－６００円＝１００円

増える、のように考えることもできます。

今回は、２０２５年度に女子中の入試で出された差集め算の問題などをご紹介しました。

１問目、２問目は定番の問題ですので、もし、正解できない問題があれば、類題を使ってできるだけ早く補強をしましょう。

３、４問目も、類題がこれまでの中学入試で出されています。

１、２問目よりも難しいのですが、倍数条件や前問からの誘導を利用して正解できると理想的だと思います。