「第７３９回　女子中の入試問題　速さ ２」

前回より、近年の女子中の入試で出された「速さ」を取り扱っています。

今回は「速さと比」の基本問題を中心に考えていきます。

１問目は、旅人算の問題です。

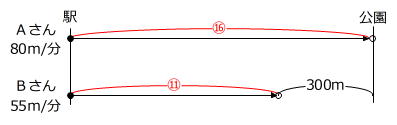
【問題】ＡさんとＢさんは、同時に駅を出発して公園まで行きます。２人の歩く速さは、Ａさんが分速８０ｍ、Ｂさんが分速５５ｍです。Ａさんが公園にとう着したとき、Ｂさんは公園の手前３００ｍのところにいました。駅から公園までの道のりは何ｍですか。

（国府台女子学院中学部　第１回　２０２５年　問題２－（３）　問題文一部変更）

【考え方】

条件は次のような線分図で表せます。

前回見た「旅人算」の公式を利用すると

（８０ｍ/分－５５ｍ/分）×（●～○の時間）＝３００ｍ

となりますから、線分図のような状態になるのは出発してから

３００ｍ÷２５ｍ/分＝１２分後

とわかります。

８０ｍ/分×１２分＝９６０ｍ

答え　９６０ｍ

（別解）

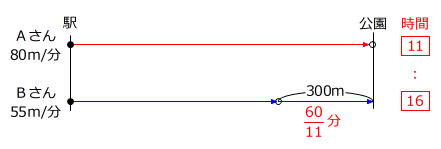
線分図解法の原則である「→に距離の比をかく」を利用することができます。

●～○の時間が２人に共通で、時間が同じときに進む距離の比と速さの比は等しいです。

速さの比　８０ｍ/分：５５ｍ/分＝１６：１１　→　距離の比　１６：１１

⑯－⑪＝３００ｍ　→　①＝３００ｍ÷５＝６０ｍ

６０ｍ×１６＝９６０ｍ

本問は、旅人算の公式や速さと比の関係を確認できる問題です。

比を利用するときは、解答例のように「時間が共通な→に着目する」や、下の別解のように「距離が共通な→に着目する」など、原則として、「共通」を利用します。

速さと比の問題が苦手なときは、本問題のように「比を使わなくても解ける問題」を使って比で解く練習をしてみましょう。

（別解）

同じ距離を進むとき、速さの比と時間の比は逆比の関係です。

３００ｍ÷５５ｍ/分＝６０/１１分　…　駅から公園までにかかる時間の差

１６□－１１□＝６０/１１分　→　１□＝１２/１１分

８０ｍ/分×（１２/１１分×１１）＝９６０ｍ

では、２問目です。

【問題】姉と妹が１００ｍ走をしたところ、姉がゴールしたとき、妹はゴールの手前１５ｍの位置にいました。２人が再びそれぞれ同じ速さで走り、同時にゴールするためには、姉はスタートの位置を何ｍ後方にすれば良いですか。ただし、２人は同時に出発するものとします。

（大妻中学校　第２回　２０２５年　問題３）

【考え方】

はじめの１００ｍ走の様子を線分図に表します。

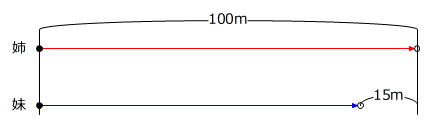
「同時マーク（同じ時刻にいる位置を示す印　●や○）」のある→に着目すると、●から○までの同じ時間に、姉は１００ｍ、妹は

１００ｍ－１５ｍ＝８５ｍ

進むことがわかります。

同じ時間に進む距離の比　姉：妹＝１００ｍ：８５ｍ＝２０：１７　…　（ア）

次に２回目の１００ｍ走の様子を線分図に表します。

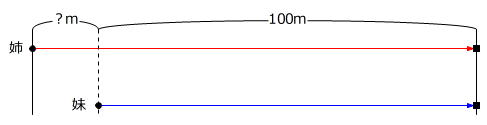
「同時に出発（●）」して「同時にゴール（■）」するという条件がありますから、時間（●～■）は同じです。

ですから（ア）より、姉が走った距離を⑳ｍとすると、妹が走った距離は⑰ｍです。

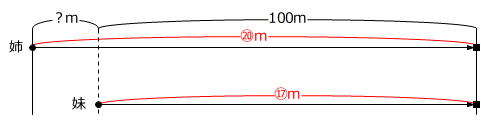
⑰ｍ＝１００ｍ　→　①ｍ＝１００/１７ｍ

？ｍ＝⑳ｍ－⑰ｍ＝③ｍ＝１００/１７ｍ×３＝３００/１７ｍ＝１７ １１/１７ｍ

答え　１７ １１/１７ｍ

本問は、速さと比の関係を確認できる問題です。

比を利用する問題であることに気づけないときは、線分図に表すことで速さの３公式が使えないことを確認しましょう。

続けて、３問目です。

【問題】Ａ地点とＢ地点を往復するとき、行きは２０分かかり、帰りは行きより毎分４５ｍ遅い速さで歩いたため、３６分かかりました。Ａ、Ｂの間の道のりは何ｍですか。

（品川女子学院中等部　算数１教科　２０２５年　問題１０　問題文一部変更）

【考え方】

往復する様子を線分図に表します。

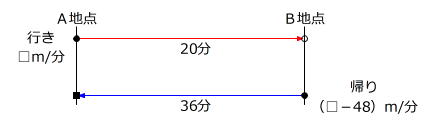
２つの→に着目すると、距離が同じです。

距離が同じとき、時間の比と速さの比は逆比の関係にあります。

行きの速さを⑨ｍ/分、帰りの速さを⑤ｍ/分とすると、その差の④ｍ/分が４８ｍ/分にあたります。

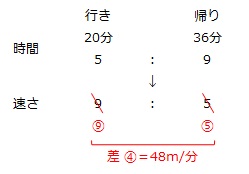
①ｍ/分＝４８ｍ/分÷４＝１２ｍ/分　→　⑨ｍ/分＝１０８ｍ/分　…　行きの速さ

１０８ｍ/分×２０分＝２１６０ｍ

答え　２１６０ｍ

本問も、速さと比の関係を確認できる問題です。

「往復する」ときは、「行きと帰りの道のりが同じ」であることに着目します。

最後は、応用問題です。

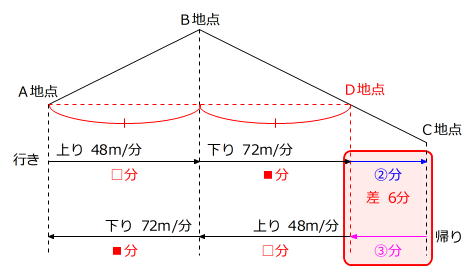
【問題】Ａ地点からＢ地点までは上り坂、Ｂ地点からＣ地点までは下り坂となっているハイキングコースがあります。平地を分速６０ｍで歩く葉子さんは、上り坂だと平地より２割遅く歩き、下り坂だと平地より２割速く歩きます。葉子さんはＡ地点を出発し、Ｂ地点を通り、Ｃ地点まで歩いて往復したところ、行きより帰りの方が６分多くかかりました。Ａ地点からＢ地点までの道のりとＢ地点からＣ地点までの道のりを比べたとき、どちらが何ｍ長いですか。

（横浜雙葉中学校　１期　２０２５年　問題１－（４））

【考え方】

６０ｍ/分×（１－０.２）＝４８ｍ/分　…　上り坂の速さ

６０ｍ/分×（１＋０.２）＝７２ｍ/分　…　下り坂の速さ

坂道を往復する様子を、線分図で表します。

行きより帰りの方が時間がかかったので、行きよりも帰りの方が上り坂が長かったことがわかります。

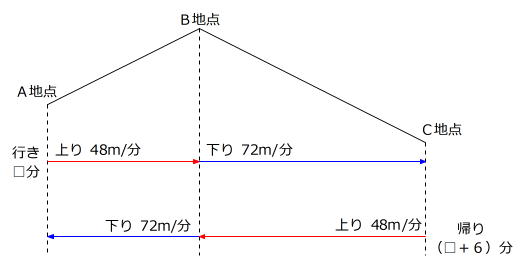
はじめに、ＡＢ間の２つの→に着目します。

２つの→の距離は同じなので、速さの比と時間の比は逆比の関係です。

このことはＢＣ間についてもいえますから、かかる時間を次のように表すことができます。

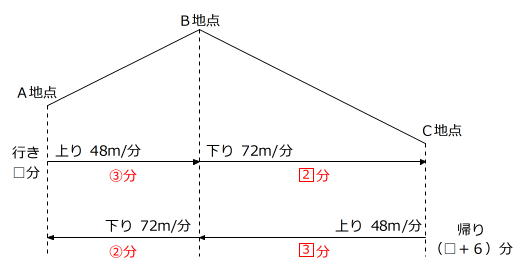
③分＋２□分＋６分＝②分＋３□分　→　①分＋６分＝１□分

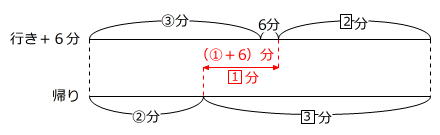
両辺を３倍すると

③分＋１８分＝３□分

となりますから、ＡからＢまでを上るよりもＣからＢまでを上る方が１８分多くかかります。

４８ｍ/分×１８分＝８６４ｍ

答え　Ｂ地点からＣ地点までの道のりの方が８６４ｍ長い

本問は、「坂道の問題」と呼ばれるものです。

坂道の問題を解くときは、解答例のように同じ区間にかかる時間の比に着目する解き方と、下の別解のように同じ距離を上り下りするときの時間の差に着目する解き方の２つが主にあります。

（別解）

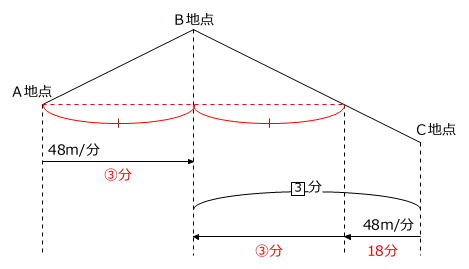
ＢＣ間にＡＢ＝ＢＤとなるようなＤ地点を考えると、ＡＤ間にかかる時間は行きも帰りも同じです。

よって、時間の差の６分はＤＣ間で生じたことになります。

ＤからＣまで下るのに②分かかるとすると、ＣからＤまで上るのに③分かかります。

③分－②分＝６分　→　③分＝１８分

４８ｍ/分×１８分＝８６４ｍ

今回は、２０２５年度に女子中で出された「速さと比」の問題をご紹介しました。

３問目までは基本レベルの問題ですから、もし、正解できないようでしたら、どこで間違えたのかを明確にして、正しい解き方をマスターしましょう。

４問目の坂道問題は応用レベルの問題です。

しかし、坂道の問題も定番問題の一つですので、既習であれば正解したいところです。

間違えたときは、解答例と別解の２つの解き方のうち、考えやすい方法から習得していきましょう。