「第７４０回　女子中の入試問題　速さ ３」

近年の女子中の入試で出された「速さ」の問題について考えています。

今回も「速さと比」の問題を中心に見ていきます。

１問目は、前回の最後にもありました「坂道の問題」です。

【問題】Ａ地点からＢ地点までは上り坂で、Ｂ地点からＣ地点までは下り坂です。花子さんは上り坂を時速３㎞、下り坂を時速４㎞で進みます。Ａ地点を出発し，Ｂ地点を通ってＣ地点までの道を往復したところ、行きは４時間３０分、帰りは４時間１５分かかりました。このとき、次の問いに答えなさい。

（１） 花子さんは、下り坂１㎞を進むよりも上り坂１㎞を進む方が何分多く時間がかかりますか。

（２） Ａ地点からＢ地点までの距離は、Ｂ地点からＣ地点までの距離より何㎞長いですか。

（３） Ａ地点からＢ地点までの距離は何㎞ですか。

（立教女学院中学校　２０２５年　問題４）

【考え方】

（１）

１㎞÷４㎞/時×６０＝１５分　…　下り坂１㎞を進むのにかかる時間

１㎞÷３㎞/時×６０＝２０分　…　上り坂１㎞を進むのにかかる時間

２０分－１５分＝５分

答え　５分

（２）

行きにかかった時間の方が帰りにかかった時間よりも多いので、行きの方が帰りよりも上り坂が長かったとわかります。

ですから、花子さんがＡＣ間を往復する様子は、次のように表すことができます。（考えやすくするため、いったん「時間」を「分単位」で表しています。）

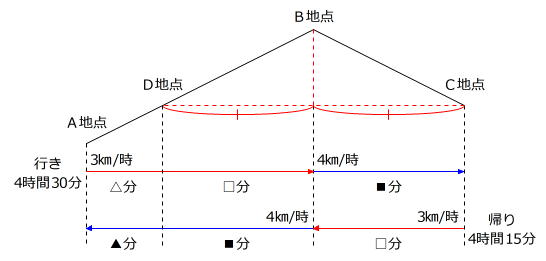
よって、往復の時間を次のような式で考えることができます。

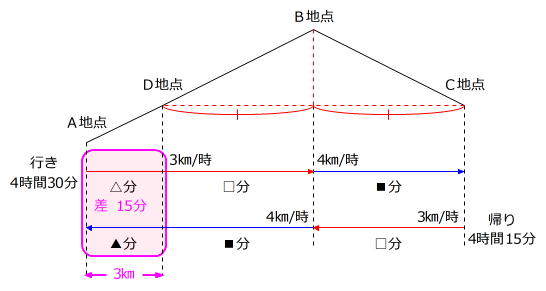
（１）より１㎞の坂道を上り下りする時間の差が５分ですから、ＡＤ間の距離は１㎞の

１５分÷５分＝３倍

の３㎞とわかり、これが ＡＢ間の距離とＢＣ間の距離の差です。

答え　３㎞

（３）

Ｄ地点からＢ地点までにかかる時間を求めます。

３㎞÷３㎞/時＝１時間　…　Ａ地点→Ｄ地点にかかる時間

４時間３０分－１時間＝３.５時間　…　Ｄ地点→Ｂ地点→Ｃ地点にかかる時間

ＤＢ間の距離とＢＣ間の距離は同じですから、速さの比と時間の比は逆比の関係です。

速さの比　　（Ｄ → Ｂ）：（Ｂ → Ｃ）＝３㎞/時：４㎞/時＝３：４

↓

時間の比　　（Ｄ → Ｂ）：（Ｂ → Ｃ）＝４：３

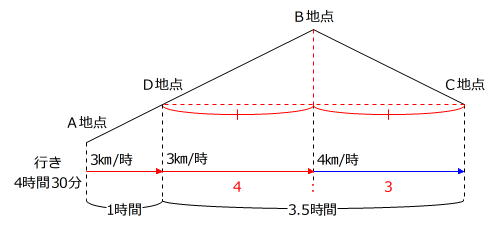
３.５時間×４/（４＋３）＝２時間　…　Ｄ地点→Ｂ地にかかる時間

ですから、Ａ地点からＢ地点までの距離は

３㎞×（１時間＋２時間）＝９㎞

です。

答え　９㎞

本問は、差集め算を利用して解く坂道の問題です。

もし、（１）が（２）誘導であることに気づけず、前回と同じようにＡＤ間にかかる時間を比で考えているときは、それでも構いませんので、答え合わせをするとき、差集め算が利用できることも確認しましょう。

２問目も、定番の「線路沿いの旅人算」問題です。

【問題】線路に沿った道を、自転車に乗り毎時１５㎞で走っている人がいます。この人は、１６分間隔で運行している電車と１２分おきにすれ違います。この電車は毎時何㎞で走っているか求めなさい。

（恵泉女学園中学校　第１回　２０２５年　問題２－（３））

【考え方】

「１６分間隔で運行」とは、ある電車がいる地点に次の電車が１６分後に来るという意味です。

ですから、「１２分おきにすれ違う」は、次のように表せます。

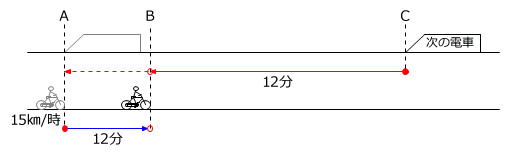
自転車はＡＢ間を、電車はＣＢ間をそれぞれ１２分で走りますから、電車がＡＢ間にかかる時間は

１６分－１２分＝４分

です。

ＡＢ間の２つの → に着目すると距離が同じですから、速さの比と時間の比は逆比の関係です。

時間の比　自転車：電車＝１２分：４分＝３：１

↓

速さの比　自転車：電車＝１：３

よって、電車の速さは

１５㎞/時×３＝４５㎞/時

です。

答え　毎時４５㎞

本問は、線路沿いのすれ違いや追い越しという定番の問題です。

電車が等間隔に走っていることを図に表すと考えやすくなります。

なお、次のような式で考えることもできます。

（電車の速さ＋自転車の速さ）×１２分＝（電車の速さ）×１６分

↓

（電車の速さ＋自転車の速さ）：（電車の速さ）＝④：③

自転車の速さ＝④－③＝①

③＝１５㎞/時×３＝４５㎞/時

では、３問目です。

【問題】地点Ａ、Ｂ、Ｃがこの順で真っ直ぐな道に沿ってあり、ＡＢ間とＢＣ間の距離の比は３：１です。ある日。愛さんは地点Ａから地点Ｃに向かって、望さんは地点Ｃから地点Ａに向かって同時に歩き始めました。望さんは地点Ｂで忘れ物に気づき、Ｃまで歩いて戻り、すぐに自転車に乗って徒歩の３倍の速さでＡに向かったところ、地点Ｂで愛さんに出会いました。愛さんと望さんの歩く速さはそれぞれ一定です。次の問いに答えなさい。

（１） 愛さんと望さんの歩く速さの比を、最も簡単な整数の比で答えなさい。

（２） 望さんが忘れ物をしなかった場合、望さんは地点Ｂより１５０ｍ進んだ場所で愛さんと出会っていました。ＡＣ間の距離を求めなさい。

（東洋英和女学院中学部　Ａ・帰国生　２０２５年　問題１１）

【考え方】

（１）

２人が進む様子は、次のように表すことができます。

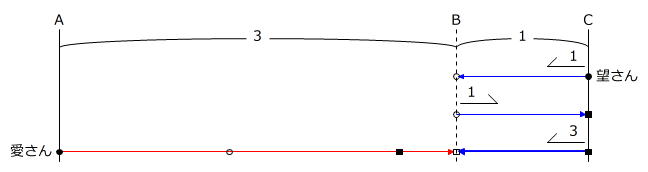
望さんの３つの → の距離はどれも同じですから、速さの比と時間の比は逆比の関係です。

速さの比　徒歩：自転車＝１：３

↓

時間の比　徒歩：自転車＝３：１

愛さんは距離が３であるＡＢ間を

③分＋③分＋①分＝⑦分

で歩き、望さんは距離が１であるＣＢ間を③分で歩きます。

線分図を見ても、愛さんと望さんについて条件が距離共通や時間共通となる → が見つかりません。

このように、条件が共通な → が見つからないときは、「速さの３公式（ここでは 距離 ÷ 時間 ＝ 速さ）」を比で利用します。

答え　９：７

（２）

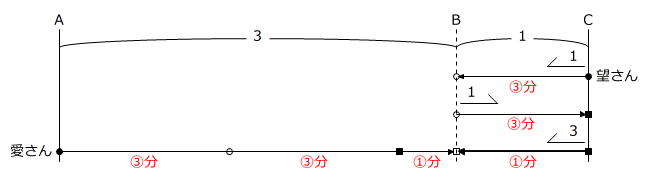
望さんが忘れ物をしなかった場合、２人が進む様子は、次のように表すことができます。

２つの → の時間が同じ（●～△）ですから、速さの比と距離の比は同じです。

ＡＣ＝⑨ｍ＋⑦ｍ＝⑯ｍ

ＡＢ＝⑯ｍ×３/（３＋１）＝⑫ｍ

⑫ｍ－⑨ｍ＝１５０ｍ　→　①ｍ＝１５０ｍ÷（１２－９）＝５０ｍ

よって、ＡＣ間の距離は

５０ｍ×１６＝８００ｍ

です。

答え　８００ｍ

本問は、比による「速さの３公式」の利用方法を確認できる問題です。

線分図を利用するときは、はじめに共通な条件をのある → を探し、そのような → が見つからないときは解答例のように比で「速さの３公式」を用いることを考えます。

今回は、２０２５年度に女子中で出された「速さと比」の応用レベルの問題をご紹介しました。

応用レベルではありますが、１問目の坂道の問題、２問目の線路沿いの旅人算は定番ですので、習い終えていたら正解させたい問題です。

３問目の「比を使った速さの３公式」も大切な解き方ですので、もし、間違えるようでしたら、すぐにおさらいをしましょう。