「第７３４回　女子中の入試問題　比と割合 １」

前回まで、５回にわたって近年の女子中の入試で出された「数と計算」について考えました。

今回からは「比と割合」の問題を取り扱っていきます。

その１回目のテーマは、「比と割合の一行問題」です。

１問目は「比例式」の問題です。

【問題】Ａ組の男子と女子の人数の比は２：３で、Ｂ組の男子と女子の人数の比は５：４です。また、Ａ組とＢ組の男子の合計と、Ａ組とＢ組の女子の合計の比は７：８です。Ａ組とＢ組の男子の人数の比をもっとも簡単な整数の比で答えなさい。

（普連土学園中学校　１日午後　２０２５年　問題（４４））

【考え方】

条件を表に整理することができます。

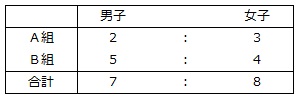
「：」で結ばれた比には、同じマークをつけることができます。

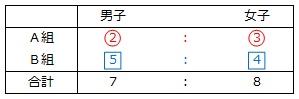
男子の合計、女子の合計について比例式を作ります。

（②＋５□）：（③＋４□）＝７：８

比例式の内項の積と外項の積は等しいです。

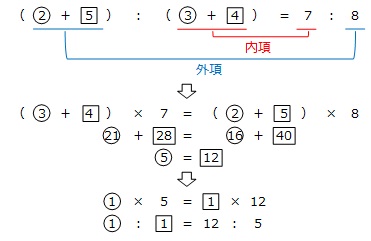
ですから、Ａ組とＢ組の男子の人数の比は

②：５□＝（１２×２）：（５×５）＝２４：２５

です。

答え　２４：２５

本問は、比例式の作り方とその計算方法を確認できる問題です。

なお、②＋５□＝７△、③＋４□＝８△として、消去算を利用する方法もあります。

２問目は「相当算」の問題です。

【問題】まおさんは、花束を作るために花を買いました。１つ目の花束には買ってきた本数の半分を使い、２つ目の花束には残りの本数の４/７を使いました。３つ目の花束には残りの９本をすべて使いました。買ってきた花は全部で何本ですか。

（三輪田学園中学校　１回午後　２０２５年　問題２－（２））

【考え方】

条件を線分図に整理することができます。

このとき、「元にする量が異なる割合」は１段下げて線分図をかくと考えやすいです。

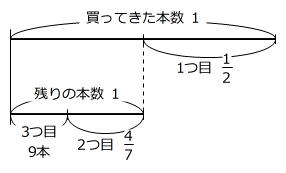
１－４/７＝３/７　→　９本が残りの本数の３/７にあたります。

（残りの本数）×３/７＝９本

（残りの本数）＝９本÷３/７＝２１本

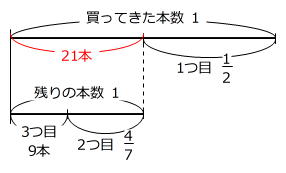
１－１/２＝１/２　→　２１本が買ってきた本数の１/２にあたります。

（買ってきた本数）×１/２＝２１本

（買ってきた本数）＝２１本÷１/２＝４２本

答え　４２本

本問は、相当算の基本を確認できる問題です。

正解できないときは、線分図をかいて考えましょう。

３問目は「２人の年令算」の問題です。

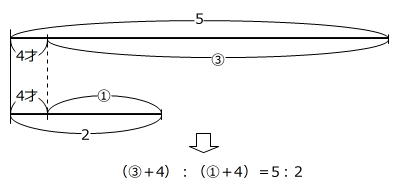
【問題】現在、母の年齢は子の年齢の３倍で、４年後に母の年齢は子の年齢の２.５倍になります。現在の母の年齢は何才ですか。

（国府台女子学院中学部　第１回　２０２５年　問題２－（２）　問題文一部変更）

【考え方】

２人の年令算では、２人の年令の差が変わらないことに着目します。

差を２と３の最小公倍数の６にそろえます。

現在③才の子どもが４年後に④才になりますから、

③才＋４才＝④才　→　①才＝４才

です。

４才×９＝３６才

答え　３６才

本問は、２人の年令算の基本を確認できる問題です。

解答例の表の他、次のような線分図に整理して解いてもよいでしょう。

４問目は「３人の年令算」の問題です。

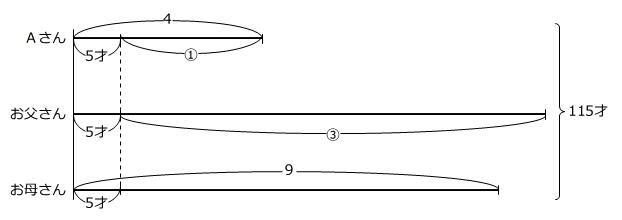
【問題】現在、Ａさんとお父さんの年齢の比は１：３です。５年後のＡさんとお母さんの年齢の比は４：９です。５年後のＡさんとお父さんとお母さんの年齢の合計は１１５歳です。現在のお父さんの年齢は何歳ですか。

（大妻中学校　第２回　２０２５年　問題６）

【考え方】

条件を表に整理することができます。

５年後のＡさんの年令を④才とすると、

現在のＡさんの年令は（④－５）才、

現在のお父さんの年令は（④－５）×３＝（⑫－１５）才、

５年後のお父さんの年令は（⑫－１５＋５）才＝（⑫－１０）才

です。

④才＋（⑫－１０）才＋⑨才＝１１５才　→　①才＝（１１５＋１０）才÷（４＋１２＋９）＝５才

５才×１２－１５＝４５才

答え　４５才

本問は、３人以上の年令算の整理方法を確認できる問題です。

３人の年令算を線分図に整理した場合、線分図のが読み取りが難しくなることがあります。

そのようなときは、表に整理し直してみるとよいでしょう。

最後は「はね上がるボール」の問題です。

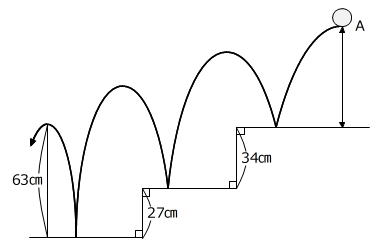
【問題】あるボールは、落とした高さの７５％まではね上がります。このボールを点Ａから落としたところ、図のように１段ずつはね、３段目で６３㎝はねました。一番上の段から点Ａまでの高さは何㎝ですか。

（東洋英和女学院中学部　Ｂ　２０２５年　問題１２）

【考え方】

（ボールを落とす高さ）×０.７５＝（ボールがはね上がる高さ）という関係を使って、最後から最初に向けて順に戻ります。

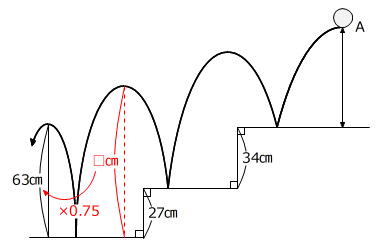
□㎝×０.７５＝６３㎝　→　□㎝＝６３㎝÷０.７５＝８４㎝

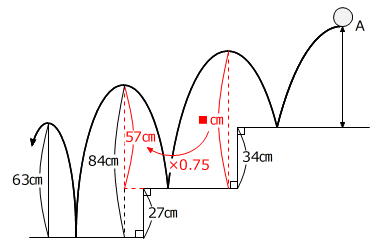
８４㎝－２７㎝＝５７㎝

■㎝×０.７５＝５７㎝　→　■㎝＝５７㎝÷０.７５＝７６㎝

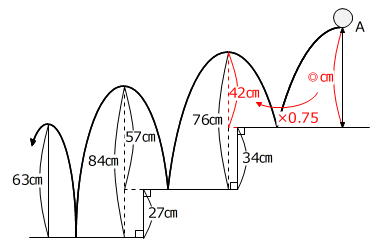
７６㎝－３４㎝＝４２㎝

◎㎝×０.７５＝４２㎝　→　◎㎝＝４２㎝÷０.７５＝５６㎝

答え　５６㎝

本問は、はね上がるボールの基本を確認できる問題です。

段ではね上がってから落ちるとき、ボールが落ちた高さから段の高さを除いた長さがはね上がる高さと等しいことに注意します。

今回は、２０２５年度に女子中の入試で出された「比と割合の一行問題」をご紹介しました。

いずれの問題も基本レベルの問題であり、また、（元にする量）×（割合）＝（比べる量）などの割合の３公式や比例式は、いろいろな問題を解くときの計算に用いる技術です。

ですから、もし、正解できない問題があれば、早急にどこで間違えたかを調べ、類題を使って正しい解き方をマスターすることが必要です。