第736回 女子中の入試問題 比と割合 3
「第736回 女子中の入試問題 比と割合 3」
前回は、近年の女子中の入試で出された「比と割合」の中から、「売買算」の問題について考えました。
今回は「食塩水」の問題を見ていきます。
1問目は基本レベルの問題です。
【問題】濃度5%の食塩水360gに、濃度の異なる食塩水200gと水を40gを加えると、7%の食塩水になりました。加えた食塩水の濃度は何%ですか。
(東洋英和女学院中学部 A・帰国生 2025年 問題3)
【考え方】
食塩水の問題は、「塩分数(分子:食塩の重さ、分母:食塩水の重さと濃さ)」を使って整理すると、食塩水の3公式(食塩水の重さ×濃さ=食塩の重さ など)を利用できるかどうかを見つけやすくなります。
このとき、水は濃度が0%の食塩水と考えます。
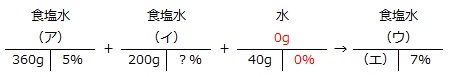
360g×0.05=18g …(ア)
360g+200g+40g=600g …(エ)
600g×0.07=42g …(ウ)
18g+(イ)+0g=42g → (イ)=24g
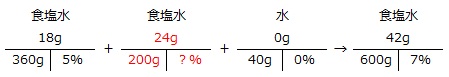
24g÷200g×100=12%
答え 12%
本問は、食塩水の3公式を確認できる基本問題です。
2問目も基本レベルの問題です。
【問題】14%の食塩水Aと2%の食塩水Bを混ぜて9%の食塩水を360g作ります。このとき、食塩水Aは何g必要ですか。
(大妻中学校 第2回 2025年 問題1-(3) 問題文一部変更)
【考え方】
塩分数を使って整理してみます。
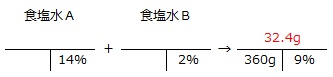
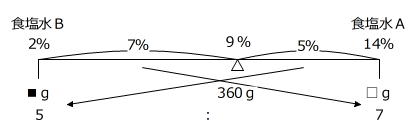
塩分数の式から食塩水の3公式を利用しにくいことがわかります(※)ので、条件を面積図(縦の長さ:食塩水の濃さ、横の長さ:食塩水の重さ、面積:食塩の重さ)に整理し直してみます。
※注:消去算を使って解くことができます。
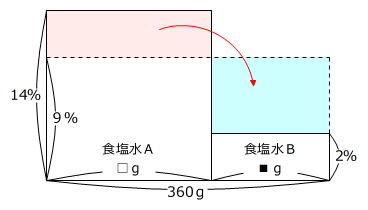
上の図のように面積図の一部を等積変形して2つの長方形の高さをそろえると、食塩水Aと食塩水Bの濃さが同じになりますから、「食塩水を混ぜた」ことになります。
このとき、赤色の長方形を水色の長方形に等積変形(面積が同じ)していますので、色をつけた2つの長方形の縦の長さの比と横の長さの比は逆比の関係です。
縦の長さの比 (14%-9%):(9%-2%)=5:7
↓
横の長さの比 □:■=7:5
□=360g×7/(7+5)=210g
答え 210g
本問は、比を使って解く基本レベルの食塩水の問題です。
比を利用する食塩水の問題が苦手なときは、本問のように塩分数の式を書いて食塩水の3公式が使えるかどうかを調べ、使えないとわかったら面積図をかくという手順で問題に取り組んでみましょう。
なお、面積図の他に、天びん図を利用しても構いません。
3問目は、食塩水のやりとりの問題です。
【問題】AとBの2つの容器にそれぞれ食塩水が400g、600g入っています。Bから100gの食塩水をくみ出してAに入れると、Aに入っている食塩水にふくまれる食塩の量は42.5gになりました。さらに、Bから140gの食塩水をくみ出してAに入れると、Bに残っている食塩水にふくまれる食塩の量は45gになりました。次の問いに答えなさい。
(1) Bの食塩水の濃さは何%ですか。
(2) Aの食塩水のはじめの濃さは何%でしたか。
(山脇学園中学校 C 2025年 問題2)
【考え方】
(1)
食塩水のやりとりの問題は、「流れ図」を使って整理することができます。
このとき、くみ出す前の食塩水の濃さ、くみ出す食塩水の濃さ、くみ出した後に残る食塩水の濃さがどれも同じであることに注意します。
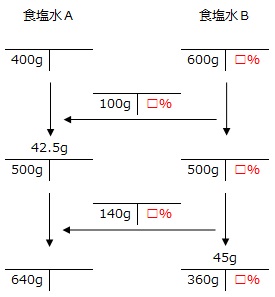
食塩水Bの最後の状態に着目します。
□%=45g÷360g×100=12.5%
答え 12.5%
(2)
(1)でわかったことを流れ図に記入します。
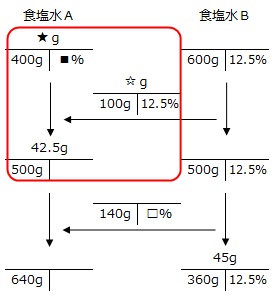
赤枠部分は「食塩水を混ぜる」ことを表していますから、塩分数の式をかくことができます。

☆g=100g×0.125=12.5g
★g+12.5g=42.5g → ★g=30g
■%=30g÷400g×100=7.5%
答え 7.5%
本問は、食塩水のやりとりの整理方法を確認できる問題です。
慣れないうちは着目する場所を見つけにくいこともあると思います。
そのような場合は、わかるところをすべて求めて考えても構いません。
最後は、3つの食塩水の混合問題です。
【問題】濃度4%の食塩水Aと濃度6%の食塩水Bと濃度10%の食塩水Cがあります。食塩水A、B、Cを2:1:1になるようにして混ぜ合わせたとき、何%の食塩水ができますか。
(品川女子学院中等部 算数1教科 2025年 問題20 問題文一部変更)
【考え方】
3つの食塩水のうち、2つの食塩水を先に混ぜ合わせることにします。
食塩水Bと食塩水Cの混ぜる割合が1:1ですから、できる食塩水の濃さは食塩水Bと食塩水Cの濃さの平均と同じです。
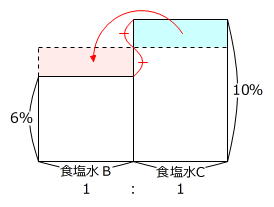
(6%+10%)÷2=8% … 食塩水Bと食塩水Cを混ぜてできる食塩水の濃さ
この食塩水と食塩水Aを混ぜ合わせます。
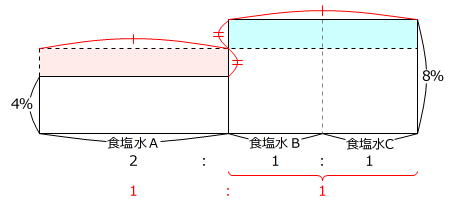
食塩水の重さの比が
2:(1+1)=1:1
ですから、混ぜてできる食塩水の濃さは、2つの食塩水の濃さの平均と同じです。
(4%+8%)÷2=6%
答え 6%
本問は、「3つの食塩水をすべて混ぜ合わせるときは、2段階でに分けて混ぜてもよい」ことを利用できる問題です。
解答例では「平均」を利用しましたが、2問目のように「等積移動」を利用してもOKです。
また、上記の他、食塩水Aと食塩水Cを混ぜると食塩水Bと同じ6%になることを利用する解き方や、次のように食塩水の重さを仮定する解き方もあります。
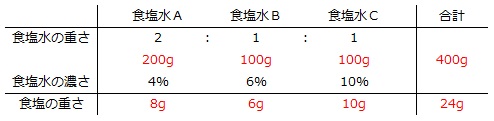
24g÷400g×100=6%
今回は、2025年度に女子中の入試で出された「食塩水」の問題をご紹介しました。
4問目は少し工夫を必要としますが、1問目から3問目は塩分数や流れ図を用いた条件の整理方法と、食塩水の3公式や面積図などの解法を確認することができる問題です。
もし、3問目までに正解できない問題があれば、間違った理由を探してすぐに修正し、これからの問題演習に備えましょう。
![]()




