第741回 女子中の入試問題 速さ 4
「第741回 女子中の入試問題 速さ 4」
ここまで、近年の女子中の入試で出された「速さ」の問題を見てきています。
今回は「速さのグラフ」の問題を取り扱います。
1問目は「旅人算とグラフ」の問題です。
【問題】学さんと友子さんは8時に家を出て、駅に向かいました。学さんは分速250mの速さで走っていましたが、駅に着いたとき忘れ物に気づき、すぐに家へ同じ速さで戻りました。友子さんが一定の速さで歩いていると、その途中で学ぶさんと8時24分にすれ違いました。その後、学さんは家で忘れ物を受け取り、すぐに駅へ分速125mの速さで向かいました。その結果、学さんと友子さんは同じ時刻に駅に着きました。グラフは、このときの時刻と2人の移動の様子を表したものです。
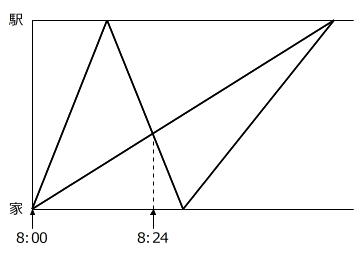
(1) 友子さんの歩く速さは分速何mですか。
(2) 家から駅までの距離は何mですか。
(鷗友学園女子中学校 第1回 2025年 問題7)
【考え方】
(1)
グラフ問題は、直角三角形に着目することが基本です。
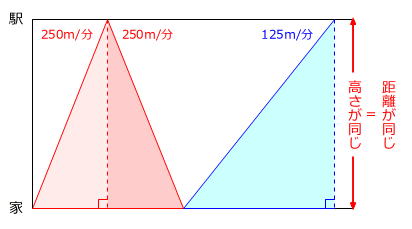
グラフの中にある3つの直角三角形は高さ、つまり、距離が同じですから、速さの比と時間の比は逆比の関係です。
速さの比 250m/分:125m/分=2:1
↓
時間の比 1:2
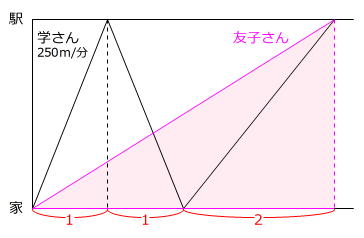
上のように時間の比をグラフに書き込むと、家から駅まで、学さんが250m/分の速さで走ると1の時間がかかり、友子さんが歩くと
1+1+2=4
の時間がかかることがわかります。
このとき2人の進む距離が家から駅までで同じですから、速さの比と時間の比は逆比の関係です。
時間の比 (学ぶさん):(友子さん)=1:4
↓
速さの比 (学さん):(友子さん)=4:1
友子さんが歩く速さを□m/分とします。
250m/分:□m/分=4:1 → □m/分=250m/分×1÷4=62.5m/分
答え 分速62.5m
(2)
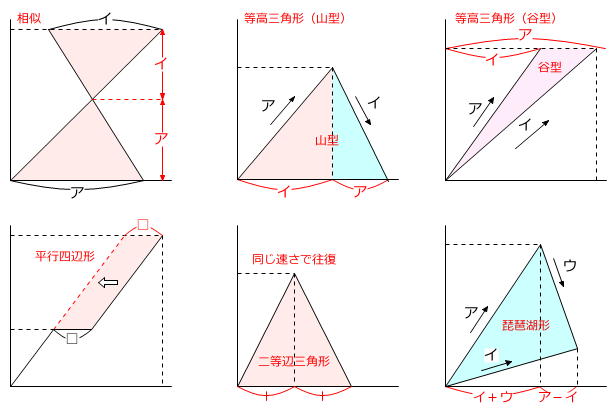
グラフ問題の着目ポイントは、基本となる直角三角形の他に、「ダイヤグラム(進行グラフ・運行グラフ)の5原則」(俗称)があります。
1 相似な三角形
2 等高三角形(高さが同じ三角形)
3 平行四辺形を探す・作る
4 二等辺三角形
5「琵琶湖形」三角形(傾いた三角形)
ここでは、「2」の等高三角形を利用してみます。
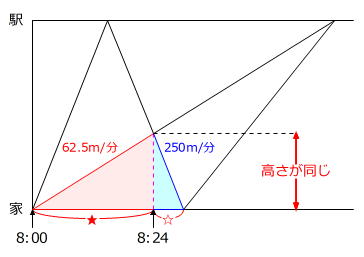
赤色の直角三角形と水色の直角三角形は高さが同じですから、速さの比と時間の比は逆比の関係です。
速さの比 62.5m/分:250m/分:=1:4
↓
時間の比 ★:☆=4:1
☆=(8:24-8:00)×1÷4=6分
なので、学さんが忘れ物を取りに家に戻った時刻は
8:24+6分=8:30
とわかります。
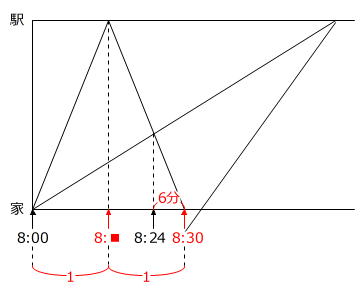
(8:30-8:00)÷2=15分 … 学さんが250m/分の速さで家から駅までにかかる時間
250m/分×15分=3750m
答え 3750m
本問は、ダイヤグラムの読み取り方を確認できる問題です。
なお、(2)では「相似な三角形」に着目する解き方もあります。
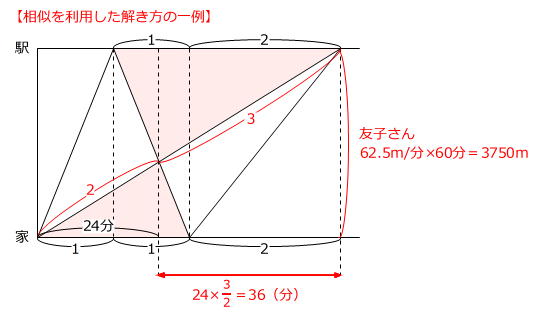
2問目は「隔たりグラフ」の問題です。
【問題】ウサギとカメが競争をすることになり、同時にスタートしました。途中ウサギは昼寝をしてしまい、目を覚ました直後に寝ぼけて逆向きに走ってしまいました。そのことに気づいたウサギは向きを変えてゴールに向かって走り、カメと同時にゴールしました。下の図はウサギとカメの間の距離と時間の関係を表したものです。後の各問いに答えなさい。ただし、ウサギとカメの走る速さはそれぞれ一定です。
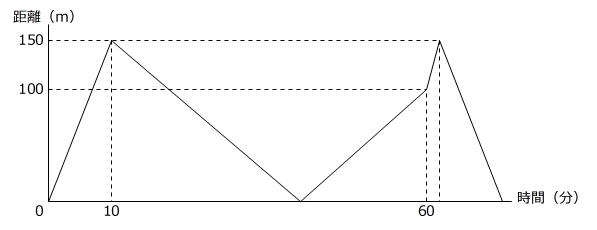
① ウサギが昼寝をしていたのは何分間ですか。
② カメが昼寝をしているウサギに追いついたのはスタートしてから何分後ですか。
③ ウサギの走る速さは分速何mですか。
④ スタートからゴールまでは何mありますか。
(共立女子中学校 2月2日 2025年 問題5)
【考え方】
①
折れ線グラフは「出来事」が生じるときに折れ曲がります。
問題文からわかる出来事を間の距離(隔たり)を表すグラフにかきます。
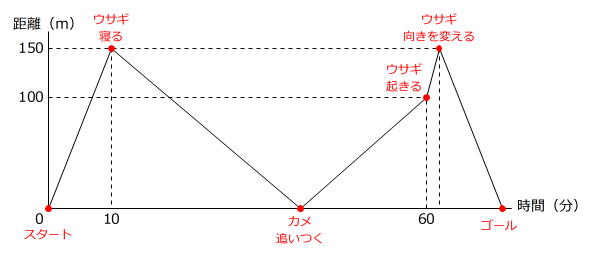
ですから、ウサギが昼寝をしていた時間は
60分-10分=50分間
です。
答え 50分間
②
「隔たりグラフ」の問題は、ダイヤグラムにかき直して考えることができます。
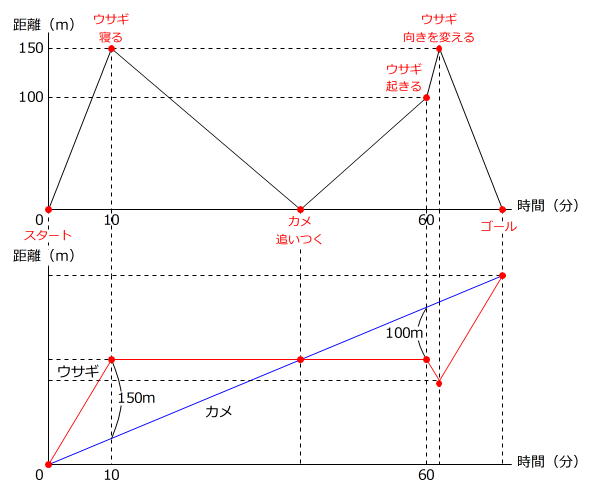
かき直したグラフを見ると、「ダイヤグラムの5原則」の「1 相似な三角形」が見つかります。
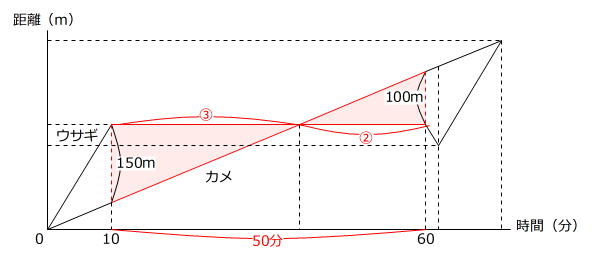
相似比が
150m:100m=3:2
ですから、
③+②=50分 → ①=50分÷(3+2)=10分
です。
よって、カメがウサギに追いついたのは出発してから
10分後+10分×3=40分後
です。
答え 40分後
③
①、②からわかることをグラフに書き込みます。
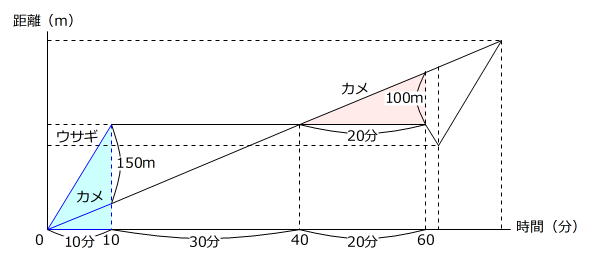
赤色の直角三角形に着目すると、カメの速さが
100m÷20分=5m/分
とわかります。
また、水色の直角三角形から、10分でウサギはカメより150m多く進むこともわかります。
同じ向きに進む旅人算の公式(速さの差)×(時間)=(隔たり)より、ウサギとカメの速さの差は
150m÷10分=15m/分
ウサギの走る速さは
5m/分+15m/分=20m/分
とわかります。
答え 分速20m
④
ウサギとカメが出発して60分後からゴールするまでの様子に着目します。
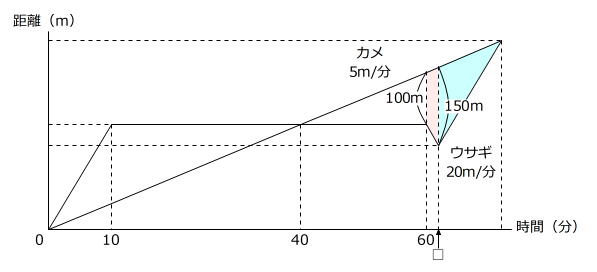
ウサギとカメの60分後の隔たりは100m、□分後の隔たりは150mですから、隔たりが
150m-100m=50m
広がっています。
逆向きに進む旅人算の公式(速さの和)×(時間)=(隔たり)より、
50m÷(20m/分+5m/分)=2分
なので
□分後=60分後+2分=62分後
です。
ウサギがここから向きを変えてカメを追いかけると
150m÷(20m/分-5m/分)=10分
で追いつきますから、ウサギとカメがゴールしたのは出発してから
62分後+10分=72分後
です。
5m/分×72分=360m
答え 360m
本問は、隔たりグラフの考え方を確認できる問題です。
解答例のようにダイヤグラムにかき直す以外に、隔たりグラフのまま考えたり、線分図にかき直して考えたりしても構いません。
今回は、2025年度に女子中で出された「速さとグラフ」の問題をご紹介しました。
グラフ問題に取り組むときは、「出来事」が生じると折れ曲がる、直角三角形に着目する、という基本の見方ができることを確認した後、旅人算を利用できる部分を見つけられることや「ダイヤグラムの5原則(下図参照)」が使えることを目指しましょう。
また、問題に応じて、線分図を利用することやグラフをかき直すことも大切なポイントです。
![]()




