「第７４７回　女子中の入試問題　平面図形 ５」

これまで、２０２５年度に女子中の入試で出された「平面図形」について考えています。

今回は「図形の移動」と「点の移動」の基本レベルの問題を見ていきます。

１問目は「平行移動」の問題です。

【問題】下の図のように、半径６㎝、中心角が３０°のおうぎ形を直線上にそってまっすぐ移動させました。このときおうぎ形の弧が通過した部分の面積は何㎠ですか。円周率は３.１４とする。

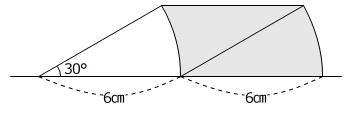
（品川女子学院中等部　算数１教科　２０２５年　問題１８　問題文一部変更）

【考え方】

求める部分は面積の公式がない図形ですから、「分ける」または「まわりから引く」を利用して面積を求めます。

ここでは「まわりから引く」を用いることにします。

「おうぎ形の弧を含む図形はおうぎ形を作る」という原則に従うと、「まわり」は右下図の図形とわかります。

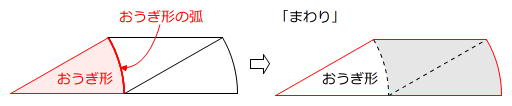
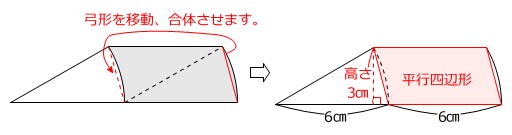
イの面積は「まわり－ア＝イ」（左下図）で求められますが、おうぎ形を平行に移動させても面積は変わりません（ア＝エ）ので、「まわり－エ＝ウ＝イ」（右下図）のように考えることができます。

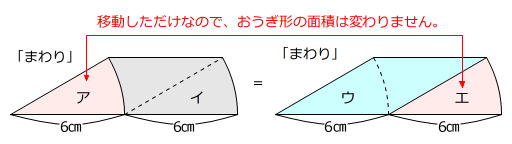
平行四辺形の底辺は６㎝で、高さは「３０度直角三角形」に着目すると３㎝とわかります。

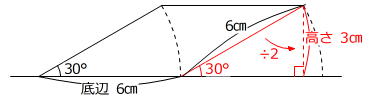
６㎝×３㎝＝１８㎠　…　ウの面積＝イの面積

答え　１８㎠

本問は、図形を移動させても面積が変化しないという考え方を確認できる問題です。

問題図に色がつけられていますから、ぜひ、正解させましょう。

なお、「分ける」を利用する場合は、次のような求め方になります。

２問目は「回転移動」の問題です。

【問題】下の図は、半径が６㎝の半円を、点Ｂを中心に６０°回転させたものです。円周率は３.１４とします。

① 色をつけた部分の周りの長さは何㎝ですか。

② 色をつけた部分の面積は何㎠ですか。

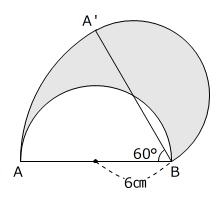
（三輪田学園中学校　第１回午後　２０２５年　問題２－（３）　問題文一部変更）

【考え方】

①

色をつけた部分は、半径が６㎝の半円の弧が２つ（赤色）と半径が１２㎝で中心角が６０度のおうぎ形の弧（青線）で囲まれています。

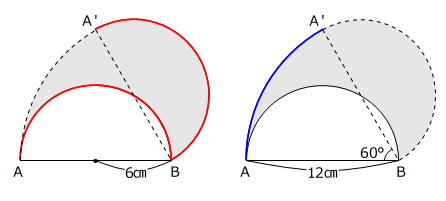
６㎝×２×３.１４×１８０度/３６０度×２＋１２㎝×２×３.１４×６０度/３６０度＝１６×３.１４＝５０.２４㎝

答え　５０.２４㎝

②

色をつけた部分は面積の公式がない図形ですから、「まわりから引く」を利用して面積を求めます。

色をつけた部分の曲線ＡＡ’はおうぎ形ＢＡＡ’の弧ですから、「まわり」は半円におうぎ形ＢＡＡ’を付け足した図形です。

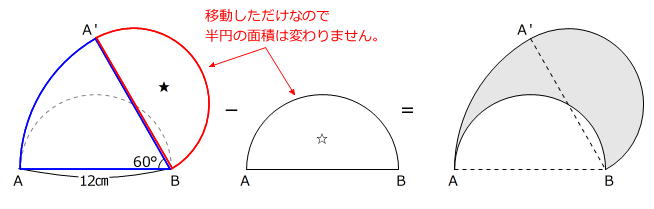
色をつけた部分の面積は「半円（赤線 ★）＋おうぎ形（青線）－半円（☆）」で求められますが、半円は回転移動させただけなので面積は変化しません（★＝☆）

ですから、色をつけた部分の面積はおうぎ形（青線）の面積と同じです。

１２㎝×１２㎝×３.１４×６０度/３６０度＝２４×３.１４＝７５.３６㎠

答え　７５.３６㎠

本問も、図形を移動させても面積が変化しないという考え方を確認できる問題です。

こちらも求める部分に色がつけられていますから、正解させたい問題です。

３問目は「転がり移動」の問題です。

【問題】１辺の長さが１２㎝の正三角形ＡＢＣがすべることなく回転します。円周率を用いるときは３.１４として答えなさい。

（１） 図の直線上を正三角形ＡＢＣが１回転するとき、点Ａが動いたあとの長さは何㎝ですか。

（２） 図の正方形の辺上と直線上を正三角形ＡＢＣが回転し、点線の正三角形の位置まで移動したとき、点Ａが動いたあとの長さは何㎝ですか。

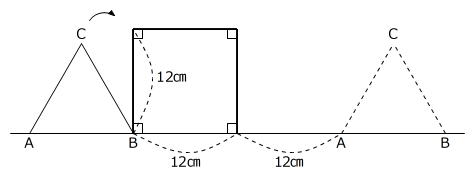
（大妻中学校　第２回　２０２５年　問題９　問題文一部変更）

【考え方】

（１）

正三角形と点Ａは次のように動きます。

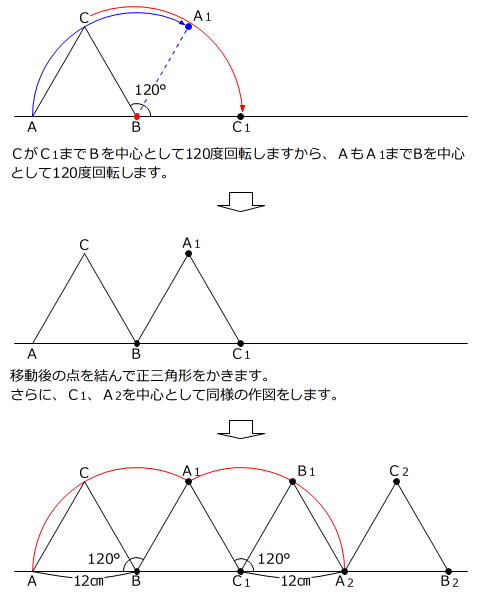
図のように、点Ａが動いたあとは、Ｂを中心とする半径が１２㎝で中心角が１２０度のおうぎ形の弧とＣ１を中心とする半径が１２㎝で中心角が１２０度のおうぎ形の弧を合わせたものです。

１２㎝×２×３.１４×１２０度/３６０度×２＝１６㎝×３.１４＝５０.２４㎝

答え　５０.２４㎝

（２）

移り変わっていく回転の中心と回転する角の大きさに注意しながら、（１）と同じように「点を移動させる　→　点を結んで正三角形をかく」を繰り返します。

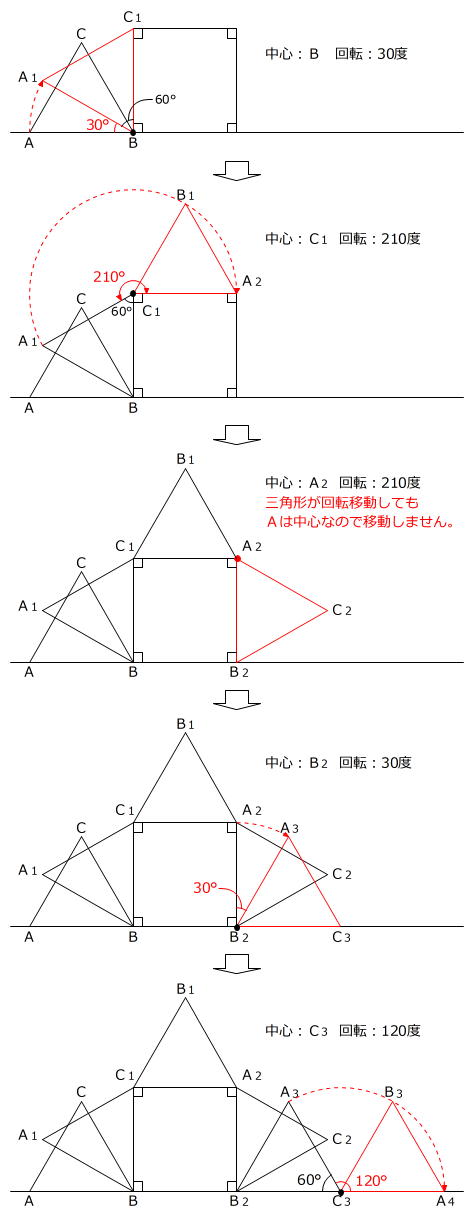
１２㎝×２×３.１４×（３０度＋２１０度＋０度＋３０度＋１２０度）/３６０度＝８１.６４㎝

答え　８１.６４㎝

本問は、転がり移動の作図を確認できる問題です。

移動の作図が苦手なようでしたら、「点だけを移動させる　→　点を結ぶ」の順に作図をしてみましょう。

最後は「点の移動」の問題です。

【問題】下の図のように、１辺が６ｍの正方形のおりの外に、長さ５ｍののび縮みしないロープで犬がつながれています。犬が動ける部分の面積は何㎡ですか。

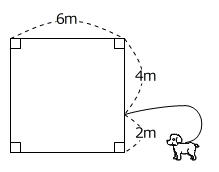
（品川女子学院中等部　算数１教科　２０２５年　問題１３　問題文一部変更）

【考え方】

ロープが「おり」とつながれている点をＡとします。

犬がＡからできるだけ図の真下の向きに進むと

５ｍ－２ｍ＝３ｍ

だけ、「おり」よりも下に行くことができます。

ですから、犬がＢからＣまで動くときに犬が通過できる部分は、半径が３ｍで中心角が９０度のおうぎ形（ア）です。

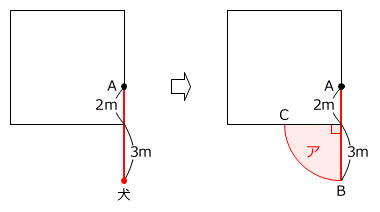
３ｍ×３ｍ×３.１４×９０度/３６０度＝９/４×３.１４㎡

次に、犬がＡからできるだけ図の真上の向きに進むと

５ｍ－４ｍ＝１ｍ

だけ、「おり」よりも上に行くことができます。

ですから、犬がＢからＤまで動くときに犬が通過できる部分は、半径が５ｍで中心角が１８０度のおうぎ形（イ）です。

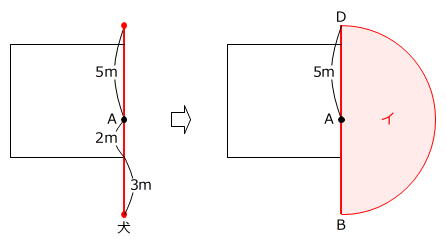
５ｍ×５ｍ×３.１４×１８０度/３６０度＝２５/２×３.１４㎡

最後に、犬がＤからＥまで動くときに犬が通過できる部分は、半径が１ｍで中心角が９０度のおうぎ形（ウ）です。

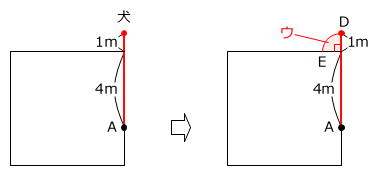
１ｍ×１ｍ×３.１４×９０度/３６０度＝１/４×３.１４㎡

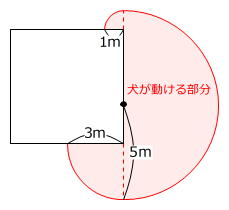
よって、犬が動ける部分の面積は

（９/４＋２５/２＋１/４）×３.１４＝４７.１㎡

です。

答え　４７.１㎡

本問は、「犬小屋の問題」とも言われる定番の問題です。

正しい作図と計算ができることを確認しましょう。

今回は、２０２５年度に女子中で出された「図形の移動」と「点の移動」の基本問題をご紹介しました。

作図や考え方はどの問題も大切です。

フリーハンドでの作図が苦手なときは、マス目の書かれたノートと定規、コンパスなどの文具を使って作図の練習をしましょう。

また、厚紙などを切って実物を作り、それを実際に動かしてみることも、苦手克服に有効です。

「図形の移動」や「点の移動」の応用問題などを解く前に、まずは、基本レベルの問題を正解できるようにしておきましょう。