第752回 女子中の入試問題 立体図形 4
「第752回 女子中の入試問題 立体図形 4」
ここまで、2025年度に女子中の入試で出された「立体図形」の問題を取り扱ってきています。
今回のテーマは「水の問題」です。
1問目は、水中におもりを入れる問題です。
【問題】ふたが付いていて密閉できる直方体の形をした容器に、水が入っています。ここに1辺2㎝の立方体の形をしたおもりPを入れます。
(1)図1のようにPを入れたら、水の中に完全に沈みました。水面の高さは何㎝高くなりましたか。
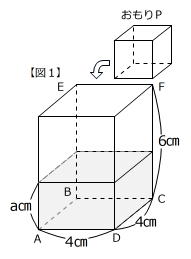
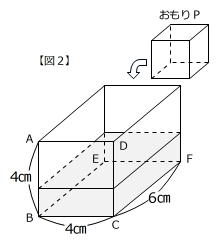
(2)図2のように、底面が長方形BCFEになるように容器の向きを変え、ここにPを入れたら、水面の高さはPの高さと等しくなりました。
① 容器に入っている水の体積は何㎤ですか。
② 図1で、aはいくつですか。
(三輪田学園中学校 第1回午後 2025年 問題3)
【考え方】
(1)
おもりPを容器に入れる前と後について、容器を正面から見た図で表します。
容器を正面から見て水面の変化を考えるときは、
・「横の長さ」の代わりに「底面積」をかく
・ おもりを容器の片側に寄せる
が作図における基本です。
4㎝×4㎝=16㎠ … 容器の底面積
2㎝×2㎝=4㎠ … おもりの底面積
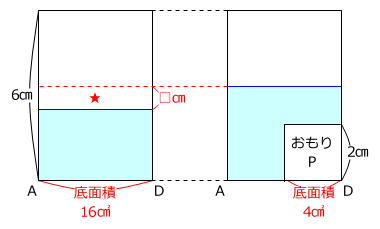
水の体積に増減はありませんから、上昇後の水面の延長線を引いてできる空間(★)の体積とおもりPの体積は同じです。
16㎠×□㎝=4㎠×2㎝ → □㎝=0.5㎝
答え 0.5㎝
(2-①)
(1)と同じように、容器を正面から見た図をかきます。
6㎝×4㎝=24㎠ … 長方形BCFEの面積(容器の底面積)
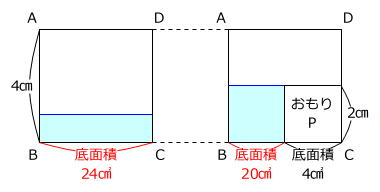
右上図から水の体積を求めることができます。
(24㎠-4㎠)×2㎝=40㎤
答え 40㎤
(2-②)
図1の水の底面積は16㎠です。
16㎠×a㎝=40㎤ → a=40÷16=2.5
答え 2.5
本問は、おもりを水に入れたときの水面の変化についての基本を確認できる問題です。
見取り図のまま考えることもできますが、正面から見た図の方がより手早くかけるので便利です。
また、もし、おもりを入れる前と後をひとつにした図をかいて間違えるようでしたら、解答例のようにおもりを入れる前と後の図を横に並べてかいて考えてみましょう。
2問目も、水中におもりを入れる問題です。
【問題】底面の円の半径が10㎝で、高さが20㎝の円柱の形をした容器Aに水が入っています。この中に、底面の円の半径が5㎝で、高さが15㎝の円柱Bを入れたときの水面の高さの変化を調べます。円柱Bの底面が、容器Aの底面にぴったり重なるように立てたところ、容器Aの水はあふれることなく、水面が3㎝上昇しました。円柱Bを入れた後の容器Aの水の深さは何㎝ですか。ただし、円周率は3.14とします。
(立教女学院中学校 2025年 問題1-(9) 問題文一部変更)
【考え方】
問題文からは、「円柱Bがすべて水中にある」のか「円柱Bの一部が水面より上にある」のかがわかりません。
そこで、いったん、「円柱Bがすべて水中にある」と仮定します。
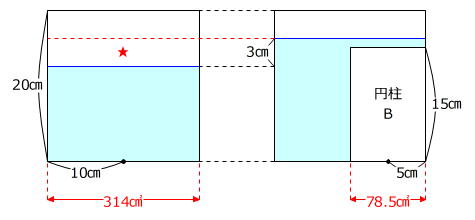
10㎝×10㎝×3.14×3㎝=942㎤ … ★の体積
5㎝×5㎝×3.14×15㎝=1177.5㎤ … 円柱Bの体積
容器Aの中に円柱Bを入れても水の体積は変化しませんから、★の体積と円柱Bの体積は等しいはずですが、計算結果は同じではありません。
ですから、「円柱Bがすべて水中にある」という仮定が間違いで、「円柱Bの一部が水面より上にある」という仮定が正しそうだと判断できます。
先ほどと同じように実際の底面積の値を用いてもよいですし、「円柱Bの一部が水面より上にある」場合は水が入っている部分を長方形で表せることから、「比」を利用して計算を簡単にするという工夫もできます。
ここでは、「比」を用いることにします。
底面の半径の比が
(容器A):(円柱B)=10㎝:5㎝=2:1
ですから、底面積の比は
(容器A):(円柱B)=(2×2):(1×1)=4:1
となり、容器Aの中に円柱Bを入れた後の水の底面積比は
4-1=3
です。
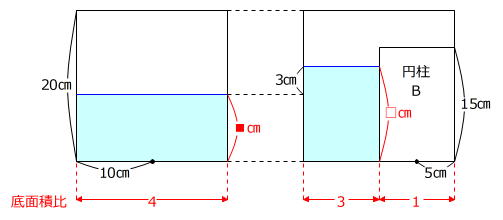
底面積4×■㎝=底面積3×□㎝ → ■:□=3:4
3:4の差の1が3㎝にあたりますから、
□㎝=3㎝×4=12㎝
です。
容器Aの中に円柱Bを入れた後の水の深さの12㎝は円柱Bの高さの15㎝よりも低いので、「円柱Bの一部が水面より上にある」という仮定が正しいとわかります。
答え 12㎝
本問には、図が与えられていないときは自分で図をかく、水面の位置を決められないときは2通りの場合を考えるという2つのポイントがあります。
水面の位置を決められないことで「手が止まる」ようでしたら、とりあえず2通りの場合のどちらか一方を試してみましょう。
今回は、2025年度に女子中の入試で出された「水の問題」の中から、「水中におもりを入れる問題」をご紹介しました。
次回は「水面の高さのグラフの問題」を取り扱う予定にしています。
このグラフの問題でも「正面から見た図」を使うことがありますので、今回の問題を見取り図で考えているときは、「正面から見た図」でも解けることを確認しましょう。
![]()




