第753回 女子中の入試問題 立体図形 5
「第753回 女子中の入試問題 立体図形 5」
ここまで、2025年度に女子中の入試で出された「立体図形」の問題を見てきています。
今回は前回に引き続き、「水の問題」の中から「水面の変化とグラフ」がテーマの問題を取り扱います。
1問目は、仕切りと排水口がある水そうの問題です。
【問題】下の図①のように、水そうの中に2つの仕切りがあります。Aの部分にある蛇口から毎分3000㎤ずつ水を入れていきます。またBの部分には排水管があり、この部分に水が入っているとき、一定の割合で水が排出されます。水を入れはじめてから30分後に一度蛇口を閉めて水を止めました。その4分後に再び蛇口を開き、毎分3000㎤ずつ水を入れました。図②は水そうの中で最も高い水面の高さと時間の関係を表したグラフです。このとき、次の問いに答えなさい。ただし、水そうや仕切りの厚さは考えないものとします。
(1) [ア]、[イ]に入る数字をそれぞれ答えなさい。
(2) 排水管からは毎分何㎤ずつ水が排出されますか。
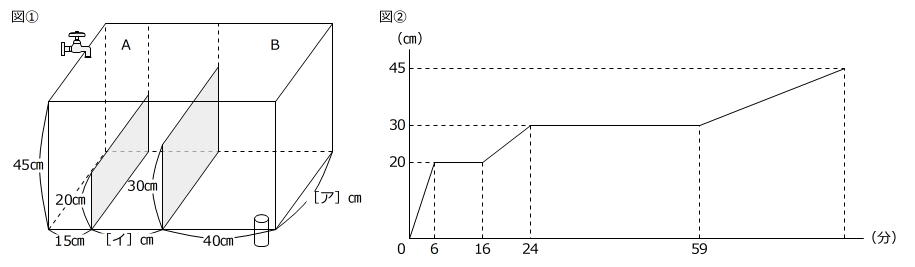
(白百合学園中学校 2025年 問題4 問題文一部変更)
【考え方】
(1)
水そうを正面から見た図をかき、グラフからわかることを記入していきます。
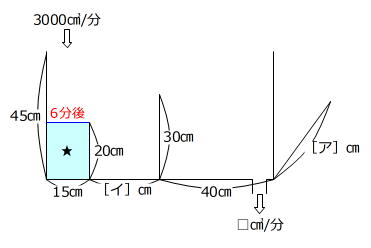
★㎤=[ア]㎝×15㎝×20㎝=3000㎤/分×6分 → ア=60
水そうの奥行きの長さがわかりましたから、蛇口から入る水の体積を、前から見たときに見える面積で表す工夫をすると、この後の計算を小さい値ですることができます。
3000㎤/分÷60㎝=50㎠/分
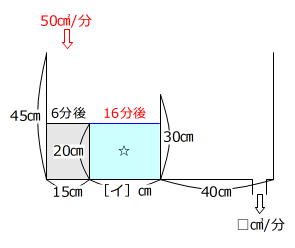
☆㎠=20㎝×[イ]㎝=50㎠/分×(16-6)分 → イ=25
答え ア 60、 イ 25
(2)
24分後から59分後までに着目します。
もし、排水されなければ
50㎠/分×(59-24-4)分=1550㎠
の水がBの部分に入りますが、実際に入っている水は
30㎝×40㎝=1200㎠
ですから、
1550㎠-1200㎠=350㎠
の水が排水されたことになります。
350㎠÷(59-24)分=10㎠/分 … 排水の速さ(前から見た面積)
面積 10㎠/分×奥行き 60㎝=体積 600㎤/分
答え 毎分600㎤
本問は仕切りや排水口のある水そうとグラフの関係の読み取りを確認できる問題です。
(2)では「もし、排水されなかったら…」という仮定を利用しましたが、排水量を□㎤/分として計算する方法もあります。
(3000-□)㎤/分×(30-24)分-□㎤/分×4分+(3000-□)㎤/分×(59-34)=60㎝×40㎝×30㎝
3000㎤/分×31分-□㎤/分×35分=72000㎤
□㎤/分=(93000㎤-72000㎤)÷35分=600㎤/分
2問目は、おもりと容器が入っている水そうの問題です。
【問題】1辺が20㎝の立方体型の水そうがあります。水そうの中に直方体の鉄の台を置き、その上に台と同じ形の水そう○あを固定し、○あの中に直方体型の水そう○いを取り付けました。○あの底面積は○いの底面積の10倍です。立方体型の水そうに図のように毎秒64㎤の割合で水を入れると、110秒で満水になりました。下のグラフは、水を入れ始めてからの時間と、辺AB部分の水面の高さとの関係を表しています。次の問いに答えなさい。
(1) 鉄の台の体積を求めなさい。
(2) [ア]、[イ]、[ウ]にあてはまる数を求めなさい。
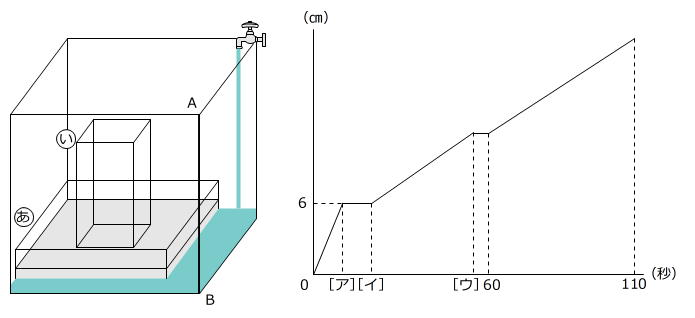
(東洋英和女学院中学部 A・帰国生 2025年 問題13 問題文一部変更)
【考え方】
(1)
時間の条件がわかっている60秒後から110秒後までに水が入る様子を、水そうを正面から見た図で表します。
20㎝×20㎝=400㎠ … 立方体型の水そうの底面積
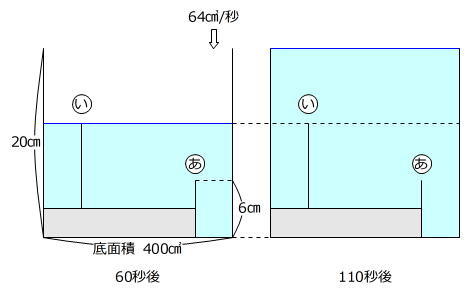
110秒後の図に着目します。
64㎤/秒×110秒=7040(㎤)… 110秒間に入った水の体積
400㎠×20㎝=8000㎤ … 立方体型の水そうの容積
満水のとき、(台の体積)+(水の体積)=(水そうの容積)ですから、台の体積は
8000㎤-7040㎤=960㎤
とわかります。
答え 960㎤
(2)
グラフが[ア]秒後に折れ曲がっていますから、直方体の台と水そう○あの高さの合計が6㎝とわかります。
台と○あは同じ形ですから、それぞれの高さは
6㎝÷2=3㎝
です。(左下図)
(1)より台の体積は960㎤ですから、台の底面積は
960㎤÷3㎝=320㎠
です。
よって、水を入れ始めたときに水が入る部分の底面積は
400㎠-320㎠=80㎠
です。(右下図)
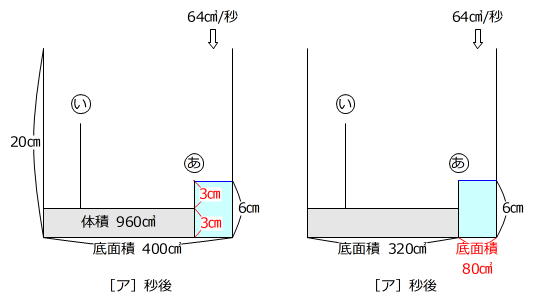
64㎤/秒×[ア]秒=80㎠×6㎝ → ア=7.5
「○あの底面積は○いの底面積の10倍」という条件より○いの底面積は
320㎠÷10=32㎠
ですから、7.5秒後から水が入る部分の底面積は
320㎠-32㎠=288㎠
です。
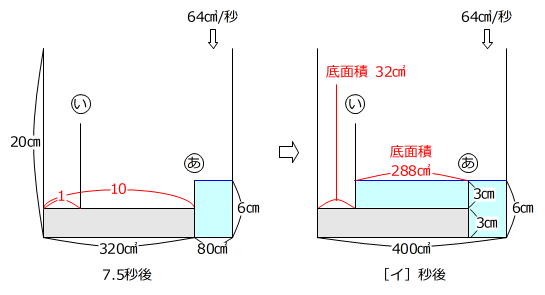
288㎠×3㎝=864㎤ … 7.5秒から[イ]秒後までに入る水の体積
864㎤÷64㎤/秒=13.5秒 → イ=7.5+13.5=21
(1)の図において、60秒後から110秒後までに入った水に着目します。
64㎤/秒×(110秒-60秒)=3200㎤ … 水の体積
400㎠×□㎝=3200㎤ → □㎝=8㎝
8㎝+■㎝+3㎝=20㎝ → ■㎝=9㎝
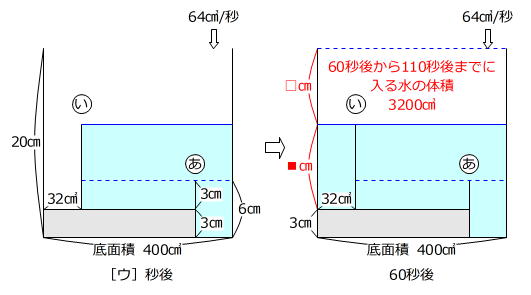
ですから、[ウ]秒後から60秒後までに入った水の体積は
32㎠×9㎝=288㎤
です。
288㎤÷64㎤/秒=4.5秒
[ウ]秒後+4.5秒=60秒後 → ウ=55.5
答え ア 7.5、 イ 21、 ウ 55.5
本問は、水そうの中に台や容器が入っているグラフの読み取りを確認できる問題です。
容器に入れている水の割合が一定ですから、水が入る部分の底面積が変化したときにグラフが曲がること、AB部分の水面の高さは水が容器の中に流れ込む間は変化しないことを利用できることがポイントです。
今回も、2025年度に女子中で出された「水の問題」をご紹介しました。
前回の水そうにおもりを入れる問題と同様に、今回の水そうの中に仕切りや容器がある問題も基本の考え方を利用して解きます。
もし、正解できないようでしたら、グラフの読み取り、給水量×時間=(直方体などの)水の体積といった、基本の考え方からチェックをしてみましょう。
![]()




