「第７５４回　女子中の入試問題　文章題 １」

２０２５年度に女子中の入試で出された問題について考えています。

今回からは「文章題」を取り扱っていきます。

１回目の今回は、「植木算」や「つるかめ算」などの問題を見ていきます。

１問目は植木算の問題です。

【問題】Ａ地点から６００ｍ離れたＢ地点まで、同じ間隔で木を植えることにしました。Ａ地点から１３ｍおきに木を植えていくと、途中で木が足りなくなり、Ｂ地点の８０ｍ手前の所までしか植えられなくなります。このとき、木は［①］本あり、Ａ地点から［②］ｍおきに木を植えると、最後の木をちょうどＢ地点に植えることができます。ただし、最初の木はＡ地点に植えるものとします。

（立教女学院中学校　２０２５年　問題１－（７）　問題文一部変更）

【考え方】

条件は次のような図に表せます。

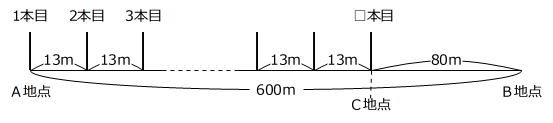
６００ｍ－８０ｍ＝５２０ｍ　…　ＡＣ間の距離

（端から端までの距離）÷（間隔）＝（間の数）です。

５２０ｍ÷１３ｍ＝４０か所…　木と木の間の数

端から端まで木を植えたとき、木の本数は間の数よりも１つ多くなります。

４０か所＋１＝４１本　→　①＝４１

Ａ地点からＢ地点まで４１本の木を端から端まで植えると、間の数は４０か所できます。

（端から端までの距離）÷（間の数）＝（間隔）という関係がありますから、

６００ｍ÷４０か所＝１５ｍ　→　②＝１５

となります。

答え　①　４１、　②　１５

本問は、植木算の基本を確認できる問題です。

もし、正解できないようでしたら、間隔、間の数、端から端までの距離の関係（間隔×間の数＝端から端までの距離 など）をチェックします。

２問目はつるかめ算の問題です。

【問題】７０円の鉛筆と１００円のボールペンと１５０円の油性ペンがあります。これらをあわせて２０本買ったところ、合計金額が１７１０円でした。このとき、鉛筆、ボールペン、油性ペンをそれぞれ何本買ったか求めなさい。

（東京女学館中学校　２月１日（午後）　２０２５年　問題２－（３））

【考え方】

３種のつるかめ算は、条件を面積図に表し、「もし鉛筆ばかりを買えば～」（最小金額）、または、「もし、油性ペンばかり買えば～」（最大金額）に着目することが、解き方の基本です。

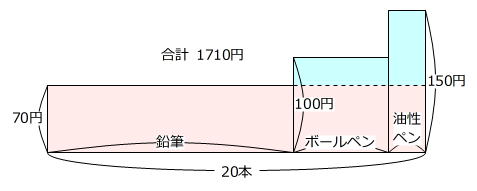
今回は、最小金額から考えることにします。

７０円×２０本＝１４００円　…　赤色部分の合計金額

最小金額（赤色部分）と実際の金額との差（水色部分）に着目します。

１７１０円－１４００円＝３１０円　…　水色部分の合計金額

１００円－７０円＝３０円

１５０円－７０円＝８０円

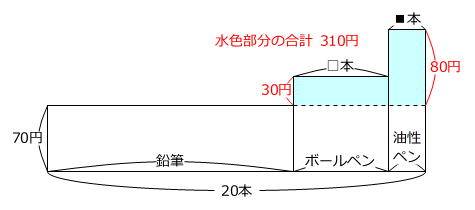
ボールペンを□本、油性ペンを■本買ったとします。

３０円×□本＋８０円×■本＝３１０円

この式にあてはまる□と■の組み合わせは、（□、■）＝（５、２）の１組だけです。

２０本－（５本＋２本）＝１３本　…　鉛筆の本数

答え　鉛筆　１３本、　ボールペン　５本、　油性ペン　２本

本問は、３種のつるかめ算の基本を確認できる問題です。

面積図をかく代わりに

７０円×☆本＋１００円×□本＋１５０円×■本＝１７１０円

のように、条件を式に表し、

３０円×□本＋８０円×■本＝１７１０円－７０円×２０本＝３１０円

と、解き進めていくこともできます。

３問目は損得のあるつるかめ算（弁償算）の問題です。

【問題】Ａさんは６０個、Ｂさんは４０個のあめ玉を持っています。コインを１回投げて表がでたらＡさんがＢさんに３個、裏がでたらＢさんがＡさんに２個あめ玉を渡します。コインを２０回投げた後、Ａさんの持っているあめ玉は５５個になりました。このとき、コインの表は何回出ましたか。

（品川女子学院中等部　算数１教科　２０２５年　問題１６　問題文一部変更）

【考え方】

弁償算は、「もし、得しかしなかったら～（損が一切なければ～）」から考えて表に整理すると、規則性を利用しやすいです。

６０＋２×２０＝１００（個）　…　裏が２０回出たときのＡさんのあめ玉

６０＋２×１９－３×１＝９５（個）　…　裏が１９回出たときのＡさんのあめ玉

６０＋２×１８－３×２＝９０（個）　…　裏が１８回出たときのＡさんのあめ玉

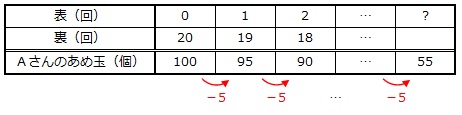
表より、表の出る回数が１回増えると、Ａさんのあめ玉が５個減るとわかります。

（１００個－５５個）÷５個＝９

よって、表の出る回数がが０回から９回増えると、Ａさんのあめ玉が５５個になります。

答え　９回

本問は、弁償算の基本を確認できる問題です。

なお、Ａさんのあめ玉の個数の増減だけに着目する解き方もあります。

６０個－５５個＝５個　…　Ａさんのあめ玉の減った個数

もし、２０回とも表がでたら

３個×２０回＝６０個

減りますから、裏が

（６０個－５個）÷（３個＋２個）＝１１回

が出たとわかります。

最後は範囲のある問題です。

【問題】１０円硬貨は１枚４.５ｇ、５円硬貨は１枚３.７５ｇあります。１０円硬貨と５円硬貨が合わせて１０００円分あり、重さが７００ｇ以上あるとき、１０円硬貨は何枚ありますか。考えられる最も多い枚数を答えなさい。

（カリタス女子中学校　第２回　２０２５年　問題１－（７）　問題文一部変更）

【考え方】

１０円硬貨と５円硬貨の合計金額が１０００円ですから、１０円硬貨と５円硬貨の枚数の組み合わせは

（１０円硬貨、５円硬貨）＝（１００枚、０枚）、（９９枚、２枚）、 … 、（０枚、２００枚）

の１０１通りがあります。

そこで、これらの組み合わせについて合計の重さを調べて表に整理し、７００ｇ以上という条件にあてはまる枚数の組を探します。

４.５ｇ×１００枚＋３.７５ｇ×０枚＝４５０ｇ

４.５ｇ×９９枚＋３.７５ｇ×２枚＝４５３ｇ

４.５ｇ×９８枚＋３.７５ｇ×４枚＝４５６ｇ

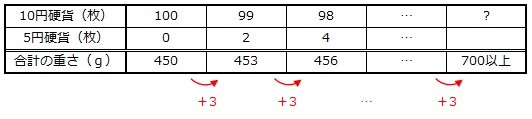
表より、１０硬貨の枚数が１枚減ると、合計の重さが３ｇ増えることがわかります。

（７００ｇ以上－４５０ｇ）÷３ｇ＝８３.３…枚以上

ですから、１０円硬貨が８４枚減ると、合計の重さが

３ｇ×８４＝２５２ｇ

増えて

４５０＋２５２＝７０２ｇ

となり、７００ｇ以上という条件を満たします。

１００枚－８４枚＝１６枚

答え　１６枚

本問は、範囲があるときの規則性の利用方法を確認できる問題です。

ポイントは、はじめに決められている合計金額から１０円硬貨と５円硬貨の枚数の組み合わせを見つけ、次に各組の重さを調べる、という手順にあります。

今回は、２０２５年度に女子中の入試で出された、植木算とつるかめ算など規則性を利用する問題をご紹介しました。

１問目の植木算は基本レベルの問題、２問目の３種のつるかめ算、３問目の弁償算はつるかめ算の中では難しい部類に入りますが、定番の問題でもありますから、これらの１～３問目の中で正解できない問題があれば、類題演習をして面積図や表の使い方を補強しましょう。

４問目は今回ご紹介した４問の中では最も難しい問題です。

解けなかったときは、何に着目するのかを確認しましょう。