「第７５９回　共学中の入試問題　数の計算」

前回まで２０２５年度に女子中の入試で出された問題について考えてきましたが、今回からは共学中の入試問題を見ていきます。

その１回目となる今回は「数の計算」を取り扱います。

１問目は工夫をすることができる計算問題です。

【問題】

次の□に当てはまる数を答えなさい。

１６×４.０２＋１.６×２９.１－０.３２×３４＝□

（広尾学園小石川中学校　第１回　２０２５年　問題１－（２））

【考え方】

１６＝１.６×１０、０.３２＝１.６×０.２ のように考えると、分配のきまりを利用できます。

　１６×４.０２＋１.６×２９.１－０.３２×３４

＝１.６×１０×４.０２＋１.６×２９.１－１.６×０.２×３４

＝１.６×（１０×４.０２＋２９.１－０.２×３４）

＝１.６×（４０.２＋２９.１－６.８）

＝１.６×６２.５

＝０.２×８×１２.５×５

＝０.２×５×８×１２.５

＝１×１００

＝１００

答え　１００

本問は、数を積の形に直すと分配のきまりを利用できる問題です。

解答例では「１.６」でくくりましたが、「１６」や「０.３２」でくくる計算方法もあります。

なお、１.６×６２.５ は、そのまま計算する、８/５×１２５/２ のように分数を利用する などでもよいと思います。

２問目以降も、工夫をして計算することができます。

【問題】次の□にあてはまる数を求めなさい。

（開智日本橋学園中学校　第１回　２０２５年　問題１－（２））

【考え方】

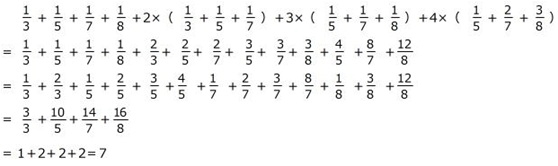
答え　７

本問は、分配のきまりを使って（　）を外す計算方法を確認できる問題です。

（　）内の分数を通分して足して和を求めているときは、解答例のような工夫ができることを確かめましょう。

では、３問目です。

【問題】次の□にあてはまる数を答えなさい。

７５＋７５＋１００＋１２５＝□×１５

（三田国際学園中学校　第１回　２０２５年　問題１－（２））

【考え方】

７５＝１５×５

１００＋１２５＝２２５＝１５×１５

を利用します。

　７５＋７５＋１００＋１２５

＝１５×５＋１５×５＋１５×１５

＝（５＋５＋１５）×１５

＝２５×１５　→　□＝２５

答え　２５

本問も１問目と同じように数を積の形に直すと分配のきまりを利用できる問題ですが、１００＋１２５＝２２５＝１５×１５ のように２数を足しておくことが工夫のポイントになっています。

４つの数を足して３７５を求めて

３７５÷１５＝２５

としてもＯＫですが、解答例のような計算ができることも確かめましょう。

なお、

７５＋７５＝１５０＝１５×１０

としても構いません。

４問目を見ていきましょう。

【問題】次の問いに答えなさい。

２０２５×２０２４＋２０２４×２０２３－２０２３×２０２５－２０２２×２０２４　を計算しなさい。

（中央大学附属中学校　第１回　２０２５年　問題１－（２））

【考え方】

　２０２５×２０２４＋２０２４×２０２３－２０２３×２０２５－２０２２×２０２４

＝２０２５×２０２４－２０２３×２０２５＋２０２４×２０２３－２０２２×２０２４

＝２０２５×（２０２４－２０２３）＋２０２４×（２０２３－２０２２）

＝２０２５×１＋２０２４×１

＝４０４９

答え　４０４９

本問は、交換のきまりを利用して順番を並べかえると分配のきまりを使えることが見つけやすくなる問題です。

「このまま計算するとものすごく大変になりそうな問題なので、もしかしたら工夫ができるかも…」と考えることができるといいですね。

５問目です。

【問題】次の□をうめなさい。

２２５－（１２×□－□×３）＝５４

ただし、□には同じ数が入ります。

（青山学院横浜英和中学校　Ａ日程　２０２５年　問題１－（２））

【考え方】

２２５－（１２×□－□×３）＝５４

２２５－（１２－３）×□＝５４

２２５－９×□＝５４

９×□＝２２５－５４＝１７１

□＝１７１÷９＝１９

答え　１９

本問は、「□」であっても同じ数であれば分配のきまりを使うことができる問題です。

正解できないようでしたら、次のような面積図で表せることを確認しましょう。

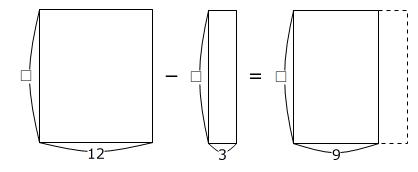
ここから、工夫の仕方が変わります。

【問題】次の□にあてはまる数を求めなさい。

（芝浦工業大学附属中学校　第１回　２０２５年　問題２－（２））

【考え方】

答え　７

本問は、部分分数分解（上記の赤色波線部分）という考え方を利用できる問題です。

（　）の中を

１/９０＋１/７２＝４/３６０＋５/３６０＝９/３６０＝１/４０

のように計算しているときは、解答例のような工夫ができることを確認します。

では、７問目です。

【問題】次の計算をしなさい。

（広尾学園中学校　第１回　２０２５年　問題１－（１））

【考え方】

答え　１/２０２０

本問も、部分分数分解を利用すると計算が簡単になる問題です。

工夫ができないようでしたら、次のような数値の小さい分数を使って、部分分数分解の練習をしましょう。

次が最後の問題です。

【問題】次の□にあてはまる最も適当な数を答えなさい。

（東邦大学付属東邦中学校　前期　２０２５年　問題１－（３））

【考え方】

答え　１/１５

本問も、部分分数分解を利用できる問題です。

帯分数の整数部分と「－４」が相殺できることポイントになっています。

今回は、２０２５年度に共学中の入試で出された「数の計算」の問題をご紹介しました。

取り扱った問題は「計算の工夫」がテーマとなっていますが、入試では順序よく計算する問題も出題されますので、これらの工夫のしかたと合わせ、速く、正確に計算できる力をつけていきましょう。