第760回 共学中の入試問題 数の性質 1
「第760回 共学中の入試問題 数の性質 1」
前回より、近年に共学中の入試で出された問題について考えています。
今回は「数の性質」の中から「商と余り」と「位取り記数法(N進法)」の問題を見ていきます。
1問目は、商と余りの関係についての問題です。
【問題】100から2025までの整数の中で、100で割り切れない整数を考えます。100で割ったときの商が余りより大きくなるような整数は何個ありますか。
(開智日本橋学園中学校 第1回 2025年 問題2-(5))
【考え方】
求める整数をA、100で割った商をB、余りをCとして、条件を式に表します。
A÷100=BあまりC
Cは100で割った余りなので0以上99以下の整数ですが、「100で割り切れない整数」という条件がありますから、Cは1以上99以下の整数です。
また、
A=101のとき → 101÷100=1あまり1
A=2025のとき → 2025÷100=20あまり25
ですから、Bは1以上20以下の整数です。
これらの商や余りが B>C となるようなAを考えます。
B=1のとき
C=0ですから、「100で割り切れない整数」という条件にあてはまりません。
B=2のとき
C=1 → A=100×2+1=201
の1個があります。
B=3のとき
C=1、2 → A=100×3+1=301、100×3+2=302
の2個があります。
…
B=19のとき
C=1、2、…、18 → A=100×19+1=1901、100×19+2=1902、…、100×19+18=1918
の18個があります。
B=20のとき
C=1、2、…、19 → A=100×20+1=2001、100×20+2=2002、…、100×20+19=2019
の19個があります。
ですから、全部で
1個+2個+…+18個+19個=(1個+19個)×19÷2=190個
あります。
答え 190個
本問は、商と余りの関係を確認できる問題です。
商と余りの関係の問題は「条件を式に表す」と、大小関係や範囲などが考えやすくなります。
なお、解答例では計算して整数Aの値を具体的に求めていますが、商が2以上20以下で余りより大きいという条件からAの個数を求めてもよいと思います。
2問目は、「余り処理」の問題です。
【問題】次の□に当てはまる数を答えなさい。
7で割ると2あまり、5で割ると3あまる300以下の整数のうち、最も大きい整数は□です。
(広尾学園小石川中学校 第1回 2025年 問題1-(4))
【考え方】
条件は次のような式で表せます。
□÷7=☆あまり2 …(ア)
□÷5=★あまり3 …(イ)
(ア)の条件を満たす□を順に書き出し、(イ)の条件を満たすかどうかを調べます。

(ア)と(イ)の2つの条件を満たす最も小さい整数は23で、(ア)を満たす整数は23から7ずつ増え、(イ)を満たす整数は23から5ずつ増えますから、次に(ア)と(イ)の条件を同時に満たす整数は23から7と5の最小公倍数である35増えた58です。

よって、(ア)と(イ)の2つの条件を満たす整数は 23+35×■ のように表せます。
そこで
23+35×■=300
とすると
■=(300-23)÷35=7あまり32
より、300以下で最も大きい整数は
23+35×7=268
とわかります。
答え 268
本問は、余り処理の基本を確認できる問題です。
正解できないようでしたら、最小の数を書き出して調べ、割る数の最小公倍数を加えていくという「余り処理」の基本解法をマスターしましょう。
その上で、余りが同じときは「最小公倍数+余り」、商と余りの差(不足)が同じときは「最小公倍数-不足」、本問のように「同じ」という関係がないときは「最小+最小公倍数」のように、条件に応じた解法も整理して習得できるといいですね。
3問目は、位取り記数法(10進法)についての問題です。
【問題】2桁の自然数がある。この自然数の各位の数の和を5倍すると、もとの数より5だけ大きくなり、十の位の数と一の位の数を入れかえると、もとの数より18だけ大きくなる。このとき、もとの自然数を求めなさい。
(広尾学園中学校 第1回 2025年 問題1-(4))
【考え方】
元の2桁の自然数(1以上の整数)の十の位の数をA、一の位の数をBとすると、元の自然数は
10×A+1×B(例:25=10×2+1×5)
十の位の数と一の位の数を入れかえてできる数は
10×B+1×A
のように表せます。
元の自然数よりも十の位の数と一の位の数を入れかえた数の方が18大きいので、
(10×B+1×A)-(10×A+1×B)=18
9×B-9×A=18
9×(B-A)=18
B-A=18÷9=2
です。
よって、元の2桁の自然数として考えられる数は
13、24、35、46、57、68、79
の7個があります。
これらの数の中から「各位の数の和を5倍すると、もとの数より5だけ大きくなり」という条件にあてはまる数を探します。
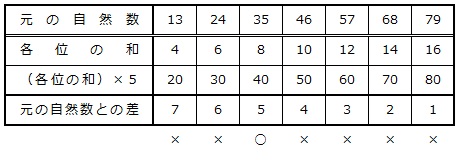
答え 35
本問は、十進数(十進法で表された数)の大きさを表す式を確認できる問題です。
「2桁の整数とその十の位の数と一の位の数を入れかえてできる整数の差は9の倍数になるので、『差が18』という条件を先に利用する」と考えることができれば、より素晴らしいです。
なお、次のように「虫食い算」を使って、A=1の場合、A=2の場合、… 、A=7の場合まで、元の自然数を順々に求めていくこともできます。
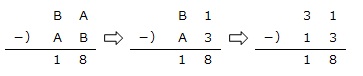
最後も、位取り記数法の問題です。
【問題】図1のマスはある規則で黒くぬりつぶされています。それぞれのマスと数字は対応しています。このとき、図2に対応する数字はいくつですか。
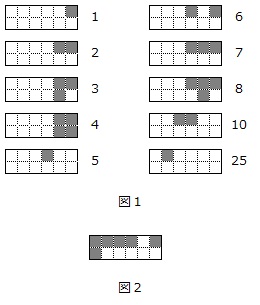
(法政大学第二中学校 第一回 2025年 問題2-(1) 問題文一部変更)
【考え方】
塗りつぶされたマスに数を書き込んでその和が「数字」と同じ値になるようにすると、数字1から数字4を表すマスは次のようになります。
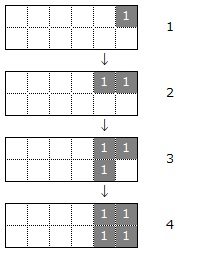
よって、5から10は次のように表せます。
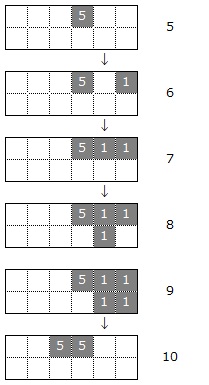
ところで、「25」は図3のように表せますから、図4は24を表していることになります。
よって、書き込む数は図5のように4個1組であることがわかります。
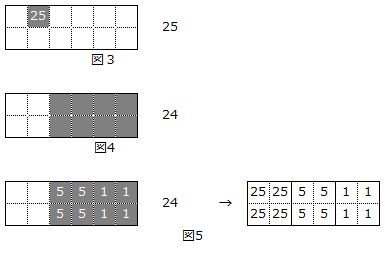
以上から、図2に対応する数字は
25×3+5×2+1=86
です。
答え 86
本問は、塗りつぶされた図から5進法の問題であることを読み取る問題です。
塗りつぶされたマスが表す数の大きさを読み取ることができれば「5進法」という言葉を意識する必要はありませんが、このような問題が位取り記数法(N進法)と関係した問題であることだけは覚えておくとよいでしょう。
今回は、2025年度に共学中で出された「商と余り」、「位取り記数法」の問題をご紹介しました。
今回の問題で使った知識は、「数の性質」の問題だけでなく、「場合の数」の問題でも必要になることがありますので、もし、正解できない問題があれば、知識の不足や覚え間違いをチェックし、修正しておきましょう。
![]()




