「第７６１回　共学中の入試問題　数の性質 ２」

近年に共学中の入試で出された問題の中から、「数の性質」がテーマの問題について考えています。

今回は「約数と倍数」の問題を見ていきます。

１問目は、最大公約数と最小公倍数に関する基本問題です。

【問題】２桁の整数Ａ、Ｂがあります。ＡとＢの最大公約数は６、最小公倍数は３６０です。ＡはＢより大きいとき、Ａにあてはまる数をすべて求めなさい。

（早稲田実業中等部　２０２５年　問題１－（２））

【考え方】

条件は、次のような「すだれ算」に整理することができます。

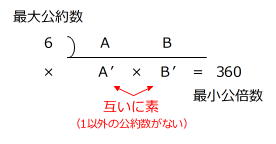
６×Ａ’×Ｂ’＝３６０　→　Ａ’×Ｂ’＝３６０÷６＝６０

また、Ａ＞Ｂ ですから、それぞれを６で割ったＡ’とＢ’についても Ａ’＞Ｂ’（Ａ’とＢ’は互いに素）です。

ですから、

（Ａ’、Ｂ’）＝（６０、１）、（２０、３）、（１５、４）、（１２、５）

の４組が考えられます。

・（Ａ’、Ｂ’）＝（６０、１）のとき

（Ａ、Ｂ）＝（３６０、６）　→　２桁の整数という条件にあてはまりません。

・（Ａ’、Ｂ’）＝（２０、３）のとき

（Ａ、Ｂ）＝（１２０、１８）　→　２桁の整数という条件にあてはまりません。

・（Ａ’、Ｂ’）＝（１５、４）のとき

（Ａ、Ｂ）＝（９０、２４）　→　２桁の整数という条件にあてはまります。

・（Ａ’、Ｂ’）＝（１２、５）のとき

（Ａ、Ｂ）＝（７２、３０）　→　２桁の整数という条件にあてはまります。

答え　９０、７２

本問は、最大公約数と最小公倍数から元の数を求める考え方を確認できる問題です。

「２桁」や「互いに素」という条件を見落とさないようにして、正解を目指しましょう。

２問目は、倍数の個数の基本問題です。

【問題】１から２０２５の整数の中で、３でも５でも割り切れない数の個数を求めなさい。

（東邦大学付属東邦中学校　前期　２０２５年　問題２－（２））

【考え方】

２０２５個の整数の中から、３または５で割り切れる整数の個数を引くことにします。

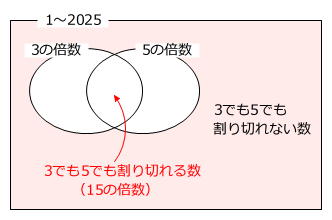
２０２５個÷３＝６７５個… ３の倍数の個数

２０２５個÷５＝４０５個… ５の倍数の個数

２０２５個÷１５＝１３５個… １５の倍数の個数

よって、３または５で割り切れる整数の個数は

６７５個＋４０５個－１３５個＝９４５個

です。

２０２５個－９４５個＝１０８０個

答え　１０８０個

本問は、倍数の個数の求め方を確認できる問題です。

なお、次のように周期算（繰り返し）の考え方を利用する解き方もあります。

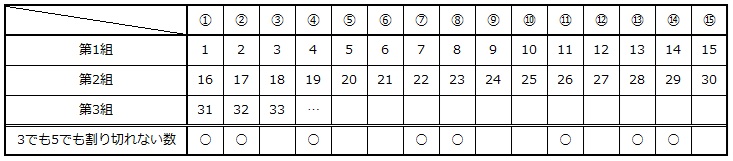
３と５の最小公倍数である１５個を１組とすると、各組の中に３でも５でも割り切れない数が８個あります。

２０２５個÷１５個＝１３５組

８個×１３５組＝１０８個

３問目は、分数についての問題です。

【問題】３/７で割っても２ ４/５をかけても整数になる数のうち、最も小さい数を求め、帯分数で表しなさい。

（慶應義塾中等部　２０２５年　問題１－（３）　問題文一部変更）

【考え方】

求める分数をＢ/Ａとすると、条件は次のような式に整理できます。

（ア）より、Ａは７と約分すると１になる数（＝７の約数）で、Ｂは３と約分すると整数になる数（＝３の倍数）とわかります。

また、（イ）より、Ａは１４と約分すると１になる数（＝１４の約数）で、Ｂは５と約分すると整数になる数（＝５の倍数）ということもわかります。

よって、Ａとして考えられる数は７と１４の公約数である１、７の２つがあり、Ｂとして考えられる数は３と５の公倍数である１５、３０、４５、…（＝１５の倍数）です。

このうち、分数が最も小さくなるのは、分母のＡが最大の７、分子のＢが最小の１５の場合です。

Ｂ/Ａ＝１５/７＝２ １/７

答え　２ １/７

本問は、約分の考え方に関する定番の問題です。

正解できないようでしたら、条件を式に整理して考えられることを確認しましょう。

４問目は、分数の約分に関する問題です。

【問題】次の□にあてはまる数を求めなさい。

下のように、分母が２０２５のこれ以上約分できない分数を小さい順に並べていきます。このとき、１９１２/２０２５は左から□番目の数です。

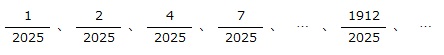
（明治大学付属明治中学校　２０２５年　第１回　問題１－（２））

【考え方】

約分は「分母と分子を同じ整数（＝□）で割って分母と分子をより小さい整数にする」という計算ですから、割る数□は分母と分子の公約数です。

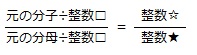
分母の２０２５を素因数分解すると

３×３×３×３×５×５

となりますから、分子が３または５の倍数である分数は約分ができるとわかります。

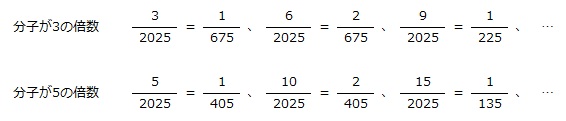
そこで、分子の３と５の最小公倍数である１５個を１組として、約分できる分数（○）と約分できない分数（×）に整理します。

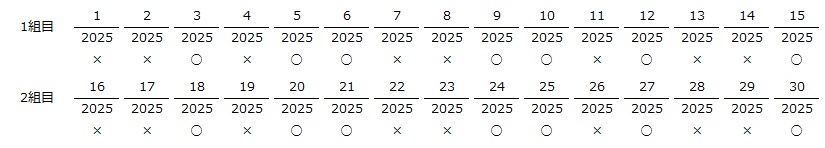
１５個１組の中に約分できない分数は８個ありますから

１９１２÷１５＝１２７あまり７

より、分子が１９１２の分数は第１２８組目の７番目の分数とわかります。

各組の１番目から７番目の分数までに約分できない分数が４個ありますから、１９１２/２０２５は

８個×１２７組＋４個＝１０２０番目

に並んでいます。

答え　１０２０番目

本問は、「約分できる分数」の考え方を利用する問題です。

正解できないようでしたら、「約分すると分子が１になる分数（＝分子が分母の約数である分数）」と区別ができること、並んでいる分数の個数がわからないときは周期算を利用することなどを確認しましょう。

今回は、２０２５年度に共学中で出された「約数と倍数」の問題をご紹介しました。

１問目から３問目までは基本レベルの問題ですから、正解できない問題があればどこで間違えているかをチェックし、すぐに修正をしましょう。

最後の問題では、「並んでいる分数の個数がわかっているときはベン図と周期算のどちらでも解ける」が「個数がわからないので周期算を利用する」といったように、条件に応じた解法を選べると理想的です。