第763回 共学中の入試問題 数の性質 4
「第763回 共学中の入試問題 数の性質 4」
ここまで、近年に共学中の入試で出された「数の性質」の問題を取り扱っています。
今回は、前回に引き続き「数の規則性」の中から、数表の問題を見ていきます。
1問目は、三角形タイプの数表の問題です。
【問題】下の図のように、ある規則にしたがって数が並んでいます。

次の①、②に答えなさい。
① 15段目の一番右にある数を求めなさい。
② 1000は何段目の左から何番目にありますか。
(早稲田実業中等部 2025年 問題2-(1))
【考え方】
①
1から整数が順に、奇数段目は右から左へ、偶数段目は左から右に向かって並んでいますので、15段目の一番右にある数は15段目の中で一番小さい数です。
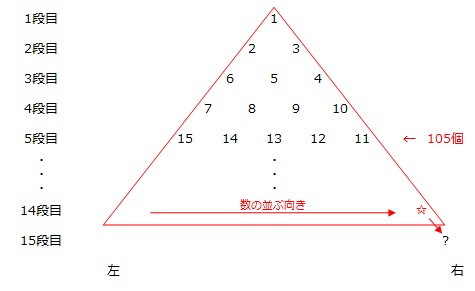
1段目から14段目までに数が全部で
1個+2個+3個+…+14個
=(1個+14個)×14÷2
=105個
並んでいますから ☆=105 となり、15段目の一番右にある数は106個目の整数である106です。
答え 106
②
1段目から□段目までに並んでいる数の個数は
(1個+□個)×□段÷2
で求められます。
(1+□)×□÷2=1000
とすると
(1+□)×□=2000
となりますので、積が2000に近い隣り合う2つの整数の組を探します。
45×44=1980
46×45=2070
より、44段目までに
(1個+44個)×44÷2=1980÷2=990個
の数が並んでいるとわかります。
よって、1000個目の整数である1000は45段目の小さい方から
1000-990=10個目
の数です。
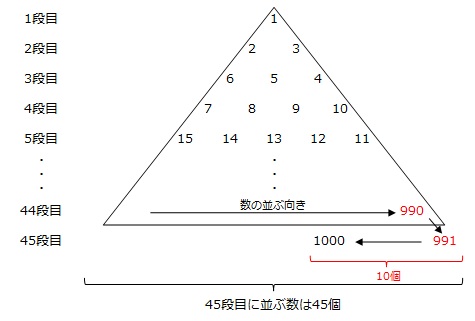
45段目は奇数段目なので数が右から左に並んでいます。
よって、45段目の右から10番目にある1000は、45段目の左から
45個-(10個-1個)=36番目
にあります。
答え 45段目の左から36番目
本問は、「三角形タイプ」の数表の基本問題です。各段の一番大きい数が「三角数」であることを利用して、正解を目指しましょう。
2問目は、正方形タイプの数表の問題です。
【問題】下の表のように、奇数を1から順にある規則にしたがってマス目に入れます。マス目に入れた奇数の場所を列と行を使って表します。例えば、11は2行3列の数字です。
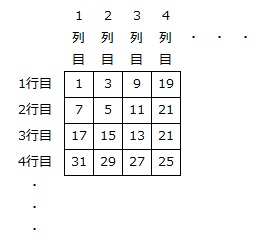
(1) 1行6列の数字は何ですか。
(2) 10行10列の数字は何ですか。
(3) 751は何行何列の数字ですか。
(開智日本橋学園中学校 第1回 2025年 問題3)
【考え方】
(1)
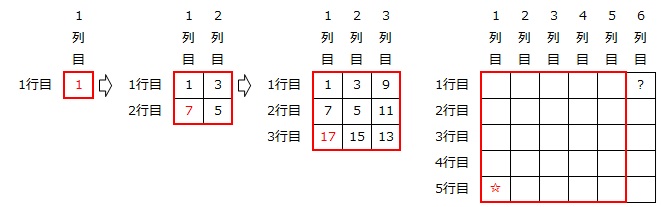
1に①、3に②、5に③、… のように、マス目に入れた奇数に番号(丸囲みの数字)をつけます。
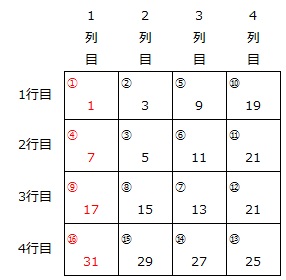
すると、1行1列に①、2行1列に④、3行1列に⑨、4行1列に⑯と、「番号」が「行」の数の平方数になっています。
また、奇数は「正方形(下図の赤枠)」を作るようにマス目に入れられますから、1行6列の数字は5行1列(下の図の☆)の次にマス目に入れる奇数です。
5行1列の奇数につけられる番号は行の数の平方数の
5×5=25
ですから、☆は1から数えて25番目の奇数である
2×25-1=49
です。
よって、その次にマス目に入れる1行6列の奇数は51です。
答え 51
(2)
10行10列の奇数は1行10列の奇数(下の図の□)から数えて10番目の数です。
1行10列の奇数(□)は9行1列の奇数(下の図の■)の次にマス目に入れる数なので、1から数えて
9×9+1=82番目
の奇数です。
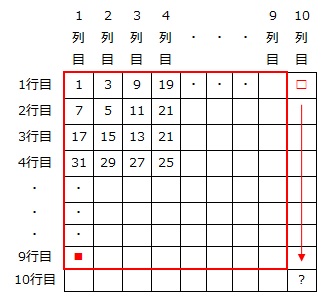
よって、10行10列の数字は1から数えて
82番目+(10行目-1行目)=91番目
の奇数である
2×91-1=181
です。
答え 181
(3)
751は1から数えて
(751+1)÷2=376番目
の奇数です。
376に近い平方数を探すと、
19×19=361
20×20=400
なので、376以下で376に最も近い平方数は361とわかります。
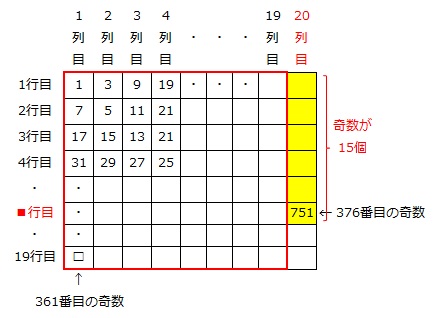
1から数えて361番目の奇数(上の図の□)は19行1列の数ですから、その奇数の
376番目-361番目=15個
あとのマス目に入れる751は15行目にあります。
です。
答え 15行20列
本問は、「正方形タイプ」の数表の基本問題です。
正解できないようでしたら、書き込む数字に「番号」をつけること、正方形タイプは「平方数」番目に着目することを確認しましょう。
3問目も、正方形タイプの数表の問題です。
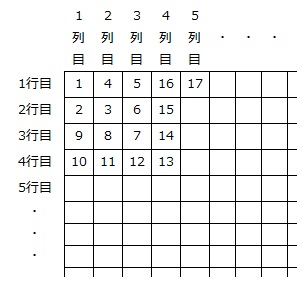
【問題】右の図のように、ます目のある大きな紙に、ある規則にしたがって数を記入していきます。また、上から○行目の左から△列目に記入する数を《○、△》と表すことにします。例えば、《3、4》=14、《4、2》=11です。このとき、次の問いに答えなさい。
(1) 次の□にあてはまる数を求めなさい。
《2、12》=□
(2) 次の[ア]、[イ]にあてはまる数をそれぞれ求めなさい。
《[ア]、[イ]》=2030
(東邦大学付属東邦中学校 前期 2025年 問題3 問題文一部変更)
【考え方】
(1)
1から整数が順に正方形を作るように並ぶ「正方形タイプ」の数表は、記入する数と番号が同じです。
そこで、記入する数のうちの平方数の位置に着目することにします。
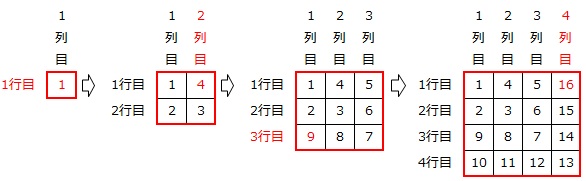
1=1×1=《1、1》
4=2×2=《1、2》
9=3×3=《3、1》
16=4×4=《1、4》
のように、奇数□の平方数は《□、1》に、偶数■の平方数は《1、■》にあります。
また、《2、12》は
《12、1》→《12、2》→ … →《12、12》→ … →《2、12》→《1、12》
の順に記入されます。
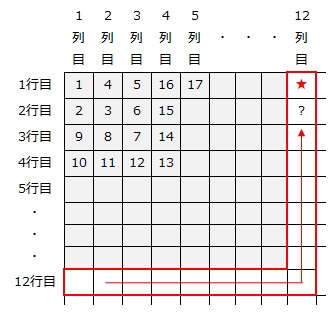
《1、12》は12の平方数である
12×12=144(上の図の★)
ですから
《2、12》=144-1=143
です。
答え 143
(2)
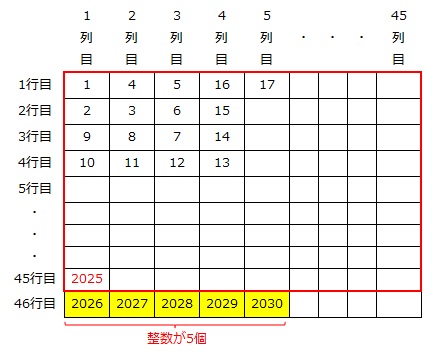
2030に近い平方数を探します。
45×45=2025
46×46=2116
より、2030は2025の5個あとに記入される数です。
2025=45×45=《45、1》
なので、2030=《46、5》です。
答え ア 46、 イ 5
本問も、「正方形タイプ」の数表の問題です。
もし、間違えるようでしたら、平方数に着目して一部を省略した数表を書き、直しをしましょう。
今回は、2025年度に共学中で出された数表の問題をご紹介しました。
数表の問題が前回の数列の問題よりも難しいと感じるようでしたら、等差数列の公式を利用できる、番号をつける、一部を省略した表を書く、三角数や平方数に着目するなどができることを確認しながら、少しずつ正解数を増やしていきましょう。
![]()




