「第７６２回　共学中の入試問題　数の性質 ３」

ここまで、近年に共学中の入試で出された問題の中から、「数の性質」がテーマの問題について考えています。

今回は「数の規則性」の問題を見ていきます。

１問目は、繰り返し（周期算）の問題です。

【問題】次の□をうめなさい。

７を５回かけた数をＡ、８を１１回かけた数をＢ、４を６回かけた数をＣとします。Ａ×Ｂ×Ｃの一の位の数は□です。

（青山学院横浜英和中学校　Ａ日程　２０２５年　問題２－（４））

【考え方】

積の一の位の数は、かけられる数とかける数の一の位の数によって決まることを利用します。

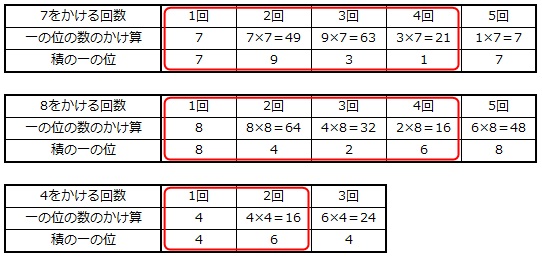
７は５回目に、８も５回目に、４は３回目に、それぞれ１回目と同じ数に戻りますから、７は４回、８も４回、４は２回をそれぞれ１セットとして繰り返すことがわかります。

ですから、

５回÷４回＝１セットあまり１回 より Ａ＝７

１１回÷４回＝２セットあまり３回 より Ｂ＝２

６回÷２回＝３セット より Ｃ＝６

です。

Ａ×Ｂ×Ｃ＝７×２×６＝８４　→　一の位の数は４

答え　４

本問は、積の一の位の数が規則的に繰り返されることを利用する問題です。

順に全て計算しているようでしたら、表などを利用して繰り返しがあることを確認しましょう。

２問目も、繰り返しの問題です。

【問題】スイッチを入れると点灯と消灯をくり返す３つのランプＡ、Ｂ、Ｃがあります。Ａのランプは１秒間点灯したあと１秒間消灯します。Ｂのランプは２秒間点灯したあと１秒間消灯します。Ｃのランプは３秒間点灯したあと１秒間消灯します。はじめ、３つのランプはすべて消灯しており、同時にスイッチを入れてすべて点灯させたあとは、規則にしたがって点灯と消灯をくり返します。３回目にすべてのランプが点灯している状態であるのは、同時にスイッチを入れた何秒後から何秒後までの間ですか。ただし、最初の点灯も回数に入れるものとします。

（東京農業大学第一高等学校中等部　第１回　２０２５年　問題３－（３））

【考え方】

繰り返しの問題は、はじめと同じ状態に戻るまでを書き出すことが基本です。

点灯と消灯を、Ａは １秒＋１秒＝２秒ごと、Ｂは ２秒＋１秒＝３秒ごと、Ｃは ３秒＋１秒＝４秒ごとに繰り返しますから、時間の最小公倍数である１２秒までを書き出します。

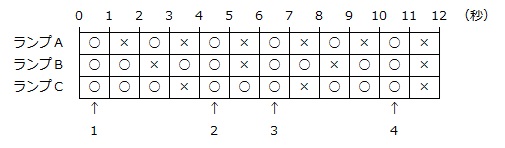
答え　６秒後から７秒後

本問は、繰り返しの定番問題です。

最小公倍数までを書き出すという基本の解き方を確認しましょう。

３問目は、群数列の問題です。

【問題】①②③④⑤…㊿のように数字が並んでいます。①●③●●⑥●●●⑩●●●●…のように黒く塗りつぶします。この規則で㊿まで繰り返すとき、見える数字をすべて足した数を求めなさい。

（広尾学園小石川中学校　第１回　２０２５年　問題２－（５））

【考え方】

黒く塗りつぶされた●が１個ずつ増えていることに着目すると

①／●③／●●⑥／●●●⑩／●●●●⑮／● …

のように１個、２個、３個、４個、… と区切ることができます。

１区切りを左から順に第１群、第２群、第３群、…とすると、それぞれの群で見えている数字は三角数（１からの整数を順に足した数）です。

第１群の個数は１個　→　①

第２群までの個数は １個＋２個＝３個　→　③

第３群までの個数は １個＋２個＋３個＝６個　→　⑥

第４群までの個数は １個＋２個＋３個＋４個＝１０個　→　⑩

第５群までの個数は １個＋２個＋３個＋４個＋５個＝１５個　→　⑮

第６群までの個数は １個＋２個＋３個＋４個＋５個＋６個＝２１個　→　㉑

第７群までの個数は １個＋２個＋３個＋４個＋５個＋６個＋７個＝２８個　→　㉘

第８群までの個数は １個＋２個＋３個＋４個＋５個＋６個＋７個＋８個＝３６個　→　㊱

第９群までの個数は １個＋２個＋３個＋４個＋５個＋６個＋７個＋８個＋９個＝４５個　→　㊺

４５の次の三角数は

４５＋１０＝５５

ですから、㊻から㊿の５個の数字は黒く塗りつぶされます。

１＋３＋６＋１０＋１５＋２１＋２８＋３６＋４５＝１６５

答え　１６５

本問は、１、１＋２＝３、１＋２＋３＝６ のような三角数の和を求める問題です。

上記はたし算の式で求めていますが、三角数は、例えば９番目の場合、（１＋９）×９÷２＝４５ のように等差数列の公式を利用して計算することもできます。

４問目も、群数列の問題です。

【問題】次のように、ある規則で左から順に数字が並んでいます。

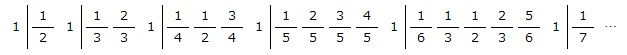
縦の棒で区切られている部分をそれぞれ群と呼ぶこととします。例えば第１群は１のみ、第２群は１/２、１となります。次の問いに答えなさい。

（１） 第１１群の５番目の数はいくつですか。

（２） 第１群の１番目から第２０群の１５番目までの数をすべてたしあわせたとき、いくつになりますか。計算の過程も含めて考え方も書きなさい。

（法政大学第二中学校　第１回　２０２５年　問題４）

【考え方】

（１）

「約分できる分数は約分をする」という規則で作られた数列であると考えると、約分をする前の数列は次のようになります。

上記のように、第□群の■番目の数は ■/□ となっていますから、第１１群の５番目の数は５/１１です。

答え　５/１１

（２）

第１群の和は １

第２群の和は １/２＋２/２＝１ １/２

第３群の和は １/３＋２/３＋３/３＝２

第４群の和は １/４＋２/４＋３/４＋４/４＝２ １/２

第５群の和は １/５＋２/５＋３/５＋４/５＋５/５＝３

第６群の和は １/６＋２/６＋３/６＋４/６＋５/６＋６/６＝３ １/２

のように、和は１から始まる公差が１/２の等差数列となっています。

１＋１/２×（１９－１）＝１０　…　第１９群の和

よって、第１群から第１９群までの和は

（１＋１０）×１９÷２＝１０４ １/２

です。

また、第２０群の１番目から１５番目の和は

１/２０＋２/２０＋３/２０＋…＋１５/２０

＝（１/２０＋１５/２０）×１５÷２

＝６

です。

１０４ １/２＋６＝１１０ １/２

答え　１１０ １/２（１１０.５）

本問は、約分された分数を含む数列の問題です。

正解できないようでしたら、約分される前の数列の問題を使って、群数列の考え方を復習します。

今回は、２０２５年度に共学中の入試で出された「数の規則性」の問題をご紹介しました

もし、間違えた問題があれば、規則が見つかるまで書き出して調べる、表を利用すると規則を見つけやすいという解き方の原則が定着できていることを確認しましょう。